Question

Calculate the effective resistance across AB.

Answer 1

Hint: When such a circuit is given to us, we have to study the connection of the resistors in the circuit, check whether they’re in series or parallel, and rearrange it for a convenient calculation approach. Then using the basic electricity formulas, we can generate required values from the simplified circuit.

Complete step by step answer:
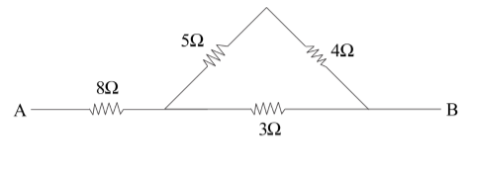
We are given a circuit with four resistors with resistance values of $8\Omega ,5\Omega ,4\Omega ,3\Omega $and this network is between two points A and B.
From the figure, we can deduce the fact that the $5\Omega $ resistor and the $4\Omega $ resistor are in series. Hence the equivalent resistance of both these resistors is given by
${{R}_{1}}=(5+4)\Omega =9\Omega $
Hence we can redraw the circuit as follows:

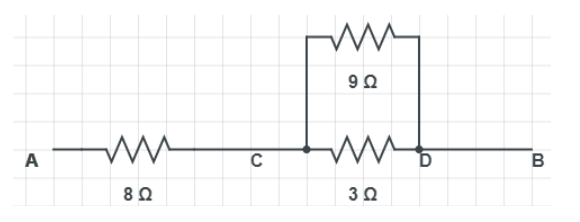
Now from the modified figure, we observe that the $9\Omega $ resistor and the $3\Omega $ resistor are in parallel,
Hence the equivalent resistance of both these resistors can be calculated by:
${{R}_{2}}=\dfrac{9\times 3}{9+3}=\dfrac{9}{4}\Omega $
Hence, we can redraw the circuit as follows:

Now from the modified figure, we find that the $8\Omega $ resistor and the $2.25\Omega $ resistor are in series,
Hence the total value of resistance of the circuit is given by
$R=(8+2.25)\Omega =10.25\Omega $
Hence, we have simplified the given circuit and we have found its net resistance value.

Note: The advantage of the usage of series circuit is the addition of devices to the circuit without restructuring the circuit. However if one element in series connection fails, the entire connection gets spoilt. Also there are chances of overheating.
The advantage of parallel circuits is the wiring. A single source can light up the entire system and if one of the elements of the system gets faulty, it doesn’t affect the system.