Question

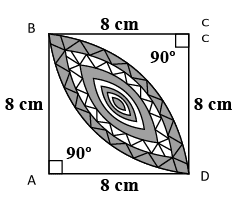
Calculate the area of the desired region in \[Fig.12.34\] common between $2$ quadrants of circle of radius \[8{\text{ }}cm\] each.

Answer 1

Hint: After seeing the figure, a student should first draw the rough figure in which he should highlight the desired region. After this, he should redraw the remaining area so that he can get an idea about the formula to be used. The student should calculate the area of the quadrant and from that, he should subtract the area of the triangle. Since the figure is symmetric, they should multiply the answer obtained by subtracting by $2$. This would be the required answer.

Complete step by step solution:
Since the given figure is symmetric over the diagonal of the square, we can find the area of the shaded region by multiplying the area of Segment BD twice.
$\therefore $Area of Shaded Region = $2 \times $Area of Segment BD.
Consider the quadrant $ABD$
Area of the quadrant is given by the formula $\dfrac{{\pi \times {r^2}}}{4}$.
Since it is a square, the side of the square becomes the radius of the quadrant,
Area of quadrant $ABD$= $\dfrac{{\pi \times {8^2}}}{4} = \dfrac{1}{4} \times 3.14 \times 8 \times 8$ = $50.24c{m^2}$
Area of $\Delta ABD $= $\dfrac{1}{2} \times b \times h$.
The height and base are the same since it is a square.
$\therefore $Area of $\Delta ABD $= $\dfrac{1}{2} \times 8 \times 8 = 32c{m^2}$.
Area of segment BD = Area of quadrant $ABD$- Area of $\Delta ABD$
                                    = $(50.24 - 32)c{m^2} = 18.24c{m^2}$
This is just one side of the shaded region, since we have the same region on the opposite side, we will have to multiply the above answer by $2$.
Area of the shaded region is $18.24c{m^2} \times 2 = 36.48c{m^2}$

Answer is $36.48c{m^2}$

Note:
In order to solve this sum correctly, the main catching point was the line of symmetry. The student had to then consider only one half of the figure and calculate the shaded region. Whenever a student gets such a type of sum It is advisable that he/she should identify if there is any symmetry and then apply the formula accordingly. For example, if in this sum we wouldn’t have applied the symmetry then it would have been practically not possible to solve the sum.