Question

Calculate the angular velocity of the earth due to its spin (rotational motion).

Answer 1

Hint:​ Angular displacement - Angular displacement is defined as “the angle in radians through which a point or line has been rotated in a specified sense (direction) about a specified axis”. It is the angle of the movement of a body in a circular path or it is the angle by which an object is rotated.
$\pi $ Radians $ = 180^\circ $
When an object is rotated to a 360° then its angular displacement will be \[2\pi \]Radians
Angular Velocity -The amount of change of angular displacement of the particle at a given time is called angular velocity.

Complete step by step solution:
Let us take the case of a solar day.
Solar day – It is the time taken by the Earth to rotate about its axis so that the Sun appears in the same position in the sky (full rotation).

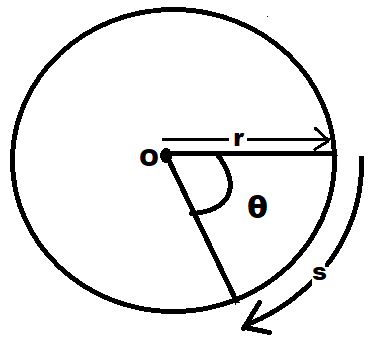
Displacement –
$s = \theta \times r$
Where,
$\theta $ is the angular displacement
s is the distance traveled by the body, and
r is the radius of the circle along which it is moving.
In simpler words, the angular displacement of an object is the distance traveled by it around the circumference of a circle divided by its radius.
Let us take a point on the surface of the circle,
Now, if that point again faces the sun after the rotation so we can say that the earth has completed one full rotation and as the point is on the surface of the earth so it has traversed a distance equal to the circumference of the earth.
Let the circumference of the earth be r
So distance (s) traversed by the point
$s = 2\pi \times r$
As, $s = \theta \times r$
$\Rightarrow \theta = 2\pi r \div r = 2\pi $ Radians
Angular velocity ( $\omega $) – The rate of change of angular displacement with respect to time
$\omega = \dfrac{{d\theta }}{{dt}}$
Where,
$d\theta $ is the change in angular displacement
$dt$ is the change in time t
Now, from the definition we can say that the displacement of the earth through a solar day is $2\pi $ radians.
Now as we know the time of a solar day is 24 hours, so we can say that it takes 24 hours for the earth to have an angular displacement of $2\pi $ radians.
$\Rightarrow $$\omega = \dfrac{{d\theta }}{{dt}}$
Here,
$d\theta $$ = 2\pi $Radians
$dt$ = $24Hours$
Now, The SI unit of angular velocity is $\dfrac{{rad}}{{\sec }}$ so we need to convert our time to seconds
$\because $1 hour = 3600 sec
$\Rightarrow $24 hours $ = 24 \times 3600$ sec
So, $\omega = \dfrac{{2\pi }}{{24 \times 3600}}$$\dfrac{{rad}}{{\sec }}$
$\Rightarrow \omega = 7.29 \times {10^{ - 5}}$$\dfrac{{rad}}{{\sec }}$

The angular speed of the earth due to its spin (rotational motion) is $7.29 \times {10^{ - 5}}$$\dfrac{{rad}}{{\sec }}$.

Note: The angular velocity of any point on the surface of the earth will be equal to the angular velocity of earth.
The planet Earth has two motions: it rotates about its axis, which gives us day and night and it revolves around the sun, giving us the seasons of the year
Angular displacement and angular velocity both are vector quantities that have both magnitudes as well as direction.
A solar day is the same as a normal day which is 24 hours.