Question

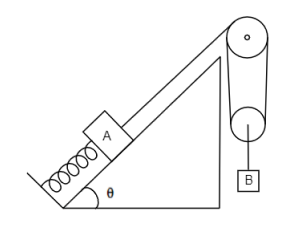
Calculate the angular frequency of the system shown in figure. Friction is absent and threads are massless. $\left( {{m}_{A}}={{m}_{B}}=m \right)$

Answer 1

Hint:The system given in this problem executes simple harmonic motion. Thus, we shall first write balanced equations of forces for the two blocks and then write the energy of the system. Further, we will differentiate that equation and put our obtained results to simplify further and compute the angular frequency.

Complete answer:
We shall assume the length of spring in equilibrium as ${{x}_{0}}$ whose spring constant is $k$. Also, let $T$ be the tension in the string. Now we will write the balanced equations of force acting on each block in equilibrium.
For block A: $k{{x}_{0}}+{{m}_{A}}g\sin \theta =T$ ……………………. (1)
For block B: $2T={{m}_{B}}g$ …………………….. (2)
Substituting the value of $T$ from (2) to (1), we get
$k{{x}_{0}}+{{m}_{A}}g\sin \theta =\dfrac{{{m}_{B}}g}{2}$ …………………….. (3)
If we displace block A by a displacement $x$from its mean position, the string gets stretched and acquires some spring energy. Both blocks A and B also gain some kinetic energy due to velocity, $v$
However, in block B, the velocity and displacement is halved, that is, $\dfrac{v}{2}$ and $\dfrac{x}{2}$ respectively. This is because it has been attached to 2 strings.
Thus the total energy of the complete system is expressed as the sum of the potential energy of spring, the kinetic energies of both blocks A and B and the potential energy of both blocks A and B due to their respective positions.
$TE=P{{E}_{spring}}+K{{E}_{A}}+K{{E}_{B}}+P{{E}_{A}}+P{{E}_{B}}$
$\Rightarrow TE=\dfrac{1}{2}k{{\left( {{x}_{0}}+x \right)}^{2}}+\dfrac{1}{2}{{m}_{A}}{{v}^{2}}+\dfrac{1}{2}{{m}_{B}}{{\left( \dfrac{v}{2} \right)}^{2}}+{{m}_{A}}gx\sin \theta -{{m}_{B}}g\left( \dfrac{x}{2} \right)$
$\Rightarrow TE=\dfrac{1}{2}k{{\left( {{x}_{0}}+x \right)}^{2}}+\dfrac{1}{2}{{m}_{A}}{{v}^{2}}+\dfrac{1}{8}{{m}_{B}}{{v}^{2}}+{{m}_{A}}gx\sin \theta -\dfrac{1}{2}{{m}_{B}}gx$
While differentiating the entire equation with respect to time, $t$, we will substitute the derivation of total energy equal to zero because according to conservation of energy the total energy remains constant.
$\Rightarrow \dfrac{d}{dt}\left( TE \right)=\dfrac{d}{dt}\left[ \dfrac{1}{2}k{{\left( {{x}_{0}}+x \right)}^{2}}+\dfrac{1}{2}{{m}_{A}}{{v}^{2}}+\dfrac{1}{8}{{m}_{B}}{{v}^{2}}+{{m}_{A}}gx\sin \theta -\dfrac{1}{2}{{m}_{B}}gx \right]$
$\Rightarrow 0=2\dfrac{1}{2}k\left( x+{{x}_{0}} \right).1+2\dfrac{1}{2}{{m}_{A}}\dfrac{dv}{dt}+2\dfrac{1}{8}{{m}_{B}}\dfrac{dv}{dt}+{{m}_{A}}g\sin \theta -\dfrac{{{m}_{B}}g}{2}$
 $\begin{align}
  & \Rightarrow 0=kx+k{{x}_{0}}+{{m}_{A}}\dfrac{dv}{dt}+\dfrac{1}{4}{{m}_{B}}\dfrac{dv}{dt}+{{m}_{A}}g\sin \theta -\dfrac{{{m}_{B}}g}{2} \\
 & \Rightarrow 0=kx+{{m}_{A}}g\sin \theta -\dfrac{{{m}_{B}}g}{2}+k{{x}_{0}}+{{m}_{A}}\dfrac{dv}{dt}+\dfrac{1}{4}{{m}_{B}}\dfrac{dv}{dt} \\
\end{align}$
From equation (3), we shall substitute $k{{x}_{0}}+{{m}_{A}}g\sin \theta =\dfrac{{{m}_{B}}g}{2}$,
$\begin{align}
  & \Rightarrow 0=\dfrac{{{m}_{B}}g}{2}-\dfrac{{{m}_{B}}g}{2}+kx+{{m}_{A}}\dfrac{dv}{dt}+\dfrac{1}{4}{{m}_{B}}\dfrac{dv}{dt} \\
 & \Rightarrow 0=kx+{{m}_{A}}\dfrac{dv}{dt}+\dfrac{1}{4}{{m}_{B}}\dfrac{dv}{dt} \\
\end{align}$
We know that $\dfrac{dv}{dt}=a$, that is, the acceleration. Putting this in our equation, we get
$\begin{align}
  & \Rightarrow 0=kx+a\left( {{m}_{A}}+\dfrac{1}{4}{{m}_{B}} \right) \\
 & \Rightarrow -kx=a\left( {{m}_{A}}+\dfrac{1}{4}{{m}_{B}} \right) \\
 & \Rightarrow a=-\dfrac{kx}{\left( {{m}_{A}}+\dfrac{1}{4}{{m}_{B}} \right)} \\
\end{align}$
Here, we have obtained our equation of the form, $a=-\sqrt{\dfrac{k}{m}}x$ or $a=-\omega x$. Comparing the coefficients of x, we get
$\Rightarrow \omega =\sqrt{\dfrac{k}{\left( {{m}_{A}}+\dfrac{1}{4}{{m}_{B}} \right)}}$
Also, it has been given that $\left( {{m}_{A}}={{m}_{B}}=m \right)$. Thus, the angular frequency is given as:
$\begin{align}
  & \Rightarrow \omega =\sqrt{\dfrac{k}{\left( m+\dfrac{1}{4}m \right)}} \\
 & \Rightarrow \omega =\sqrt{\dfrac{4k}{5m}} \\
\end{align}$
Therefore, the angular acceleration of the system is $\sqrt{\dfrac{4k}{5m}}$.

Note:
The angular frequency is obtained by the basic equation of simple harmonic motion where the acceleration is directly proportional to negative of the displacement of the body. Also, we must know how to express the kinetic as well as potential energies of any body.