Question

Calculate the angle between two vectors \[F\] and \[\sqrt{2}F\] so that the resultant force is \[\sqrt{10}F\] \[N\] .

Answer 1

Hint:When two vectors having certain magnitudes and direction and present in the same plane are represented by the two sides of a parallelogram, in a way that the tails of the two vectors form a vertex of the parallelogram, then the diagonal of the parallelogram formed will be the resultant of the two vectors. This is known as the parallelogram law of vector addition.

Complete step-by-step solution:
Depicting the above parallelogram law in a diagram,
According to this, \[\overset{\to }{\mathop P}\,\] and \[\overset{\to }{\mathop Q}\,\] are two vectors, aligned as the parallelogram law of vector addition states, then according to the law, the diagonal of the parallelogram ABOD \[\overrightarrow{R}\] will be the resultant of the two vectors.

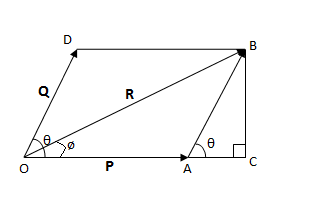
From the above diagram, we can deduce the following relations:
 \[\begin{align}
  & \overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q} \\
 & \Rightarrow {{\overrightarrow{OB}}^{2}}={{\overrightarrow{OC}}^{2}}+{{\overrightarrow{BC}}^{2}} \\
\end{align}\]
Also, we can deduce that
 \[\begin{align}
  & \overrightarrow{AC}=\overrightarrow{AB}\cos \theta \\
 & \overrightarrow{BC}=\overrightarrow{AB}\sin \theta \\
\end{align}\]
The magnitude of the resultant vector is thus,
\[\begin{align}
  & {{R}^{^{2}}}={{(P+Q\cos \theta )}^{2}}+{{(Q\sin \theta )}^{2}} \\
 & R=\sqrt{{{P}^{2}}+2PQ\cos \theta +{{Q}^{2}}} \\
\end{align}\]
As per the given problem, the two vectors are, \[F\] and \[\sqrt{2}F\] the resultant vector is \[\sqrt{10}F\].
Substituting the given data in the above formula for resultant vector,
\[\sqrt{10}F=\sqrt{{{F}^{2}}+(2\times F\times \sqrt{2}F\times \cos \theta )+{{(\sqrt{2}F)}^{2}}}\]
Squaring on both sides, we get
\[\begin{align}
  & 10{{F}^{2}}={{F}^{2}}+2\sqrt{2}{{F}^{2}}\cos \theta +2{{F}^{2}} \\
 & \Rightarrow 7{{F}^{2}}=2\sqrt{2}{{F}^{2}}\cos \theta \\
 & \Rightarrow \cos \theta =0.707 \\
 & \Rightarrow \theta ={{45}^{\circ }} \\
\end{align}\]
Hence, the angle between the two given vectors is \[{{45}^{\circ }}\] .
The direction of the resultant vector is given by \[\phi ={{\tan }^{-1}}(\dfrac{Q\sin \theta }{P+Q\cos \theta })\].

Note:- An alternative to the parallelogram law of vector addition is the triangle law of vector addition where the two vectors are represented by the two sides of a triangle and the third side represents the resultant of the vectors. The parallelogram law also states that the sum of squares of the four sides of the parallelogram is equal to the sum of squares of the two diagonals.