Question

Calculate $ \sin (2\arctan 2) $

Answer 1

Hint: Here the question is related to the trigonometry where it contains the sine and tan function. The question is exactly related to inverse trigonometry because we see “arctan” which means tan inverse. Hence by applying the inverse trigonometry we can find the result.

Complete step-by-step answer:
The question is given as $ \sin (2\arctan 2) $
Now let us consider the $ x = \arctan 2 $ --- (1)
We know that the inverse is also called an arc. Therefore the equation (1) can be written as
 $ x = {\tan ^{ - 1}}(2) $ --------- (2)
The equation (2) can be written as
 $ \tan x = 2 $ ---------- (3)
By the considering the triangle we can define the $ \tan x $
Let us consider the right angled triangle ABC

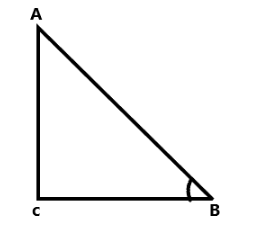
 $ \tan x = \dfrac{{opposite}}{{adjacent}} = \dfrac{{AC}}{{BC}} $
 $ \Rightarrow \dfrac{2}{1} = \dfrac{{AC}}{{BC}} $
Therefore the value of AC=2 and BC=1
By applying the Pythagoras theorem we have
 $
  A{B^2} = A{C^2} + B{C^2} \\
   \Rightarrow A{B^2} = {(2)^2} + {(1)^2} \\
   \Rightarrow A{B^2} = 4 + 1 \\
   \Rightarrow A{B^2} = 5 \\
   \Rightarrow AB = \sqrt 5 \;
  $
Hence the length of the AB= $ \sqrt 5 $
Now we have to find the value of $ \sin 2x $
We know the trigonometry formula that is $ \sin 2x = 2.\sin x.cosx $ ----(4)
By considering the triangle we can find the value of sine and cosine.
So we have
 $ \sin x = \dfrac{{opposite}}{{hypothesis}} = \dfrac{{AC}}{{AB}} $
As we know the value. Substituting we have
 $ \Rightarrow \sin x = \dfrac{2}{{\sqrt 5 }} $ ---- (5)
 $ \cos x = \dfrac{{adjacent}}{{hypothesis}} = \dfrac{{BC}}{{AB}} $
As we know the value. Substituting we have
 $ \Rightarrow \cos x = \dfrac{1}{{\sqrt 5 }} $ ---- (6)
Substituting the equation (5) and equation (6) in equation (4) we have
 $
  \sin 2x = 2\sin x.\cos x \\
   \Rightarrow \sin 2x = 2 \times \dfrac{2}{{\sqrt 5 }} \times \dfrac{1}{{\sqrt 5 }} \\
   \Rightarrow \sin 2x = \dfrac{4}{5} \;
  $
Hence we have obtained the required result.
Therefore, the value of $ \sin (2\arctan 2) = \dfrac{4}{5} $
So, the correct answer is “ $ \dfrac{4}{5} $ ”.

Note: The inverse is also called an arc. This word is used in question very rare. In most questions they will ask directly like find the inverse. The sine function, cosine function and tan function are defined by considering the right angled triangle. Hence we know about the Pythagoras theorem and to which type of triangle it is applicable.