Question

Calculate $\oint{\overrightarrow{B}\cdot \overrightarrow{dl}}$ over following loops. Here the direction in which integration has to be performed has been represented by arrows.
A.

 B.

C.

 

D.

Answer 1

Hint: The current inside the loop is having a direction into We can say that in order to attain stable equilibrium the plane should be in a vertical direction. The integral of the dot product of the magnetic field and the length element over the loops represent that the plane is carrying the current.

Complete answer:
In the first figure we can see that there are two currents. One is outside the loop which will not be producing any kind of magnetic field. Therefore we can neglect it. The other one which is inside the loop is having a current direction going outside the loop. Therefore the magnetic field produced will be anticlockwise in direction. Therefore we can write that,
$\oint{\overrightarrow{B}\cdot \overrightarrow{dl}}={{\mu }_{0}}{{i}_{1}}$
Now for the second figure also the current outside the loop can be neglected. Here the magnetic field produced will be in the anticlockwise direction. As the direction of current is negative, we can write that,
$\oint{\overrightarrow{B}\cdot \overrightarrow{dl}}=-{{\mu }_{0}}{{i}_{2}}$
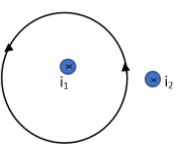
For the third loop we can see that the current in both the smaller loop is having direction into the sheet. But the current produced is in anticlockwise direction. Therefore we can write that,
$\oint{\overrightarrow{B}\cdot \overrightarrow{dl}}=-{{\mu }_{0}}i-{{\mu }_{0}}i=-2{{\mu }_{0}}i$
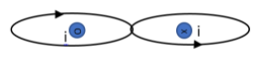
For the fourth one we can say the first smaller loop is having a positive value of ${{\mu }_{0}}{{i}_{1}}$ and in the second, third and fourth loop it is negative. Therefore we can write that,
$\oint{\overrightarrow{B}\cdot \overrightarrow{dl}}=-{{\mu }_{0}}i+{{\mu }_{0}}i-{{\mu }_{0}}i-{{\mu }_{0}}i=-2{{\mu }_{0}}i$
Therefore the values for the integral in all the cases have been found.

Note:
The loop has been suspended in a vertical direction. The vertical direction of the loop represents that the plane is normal to the magnetic meridian. Both the magnetic meridian and the plane are in stable equilibrium. Therefore we can say that to attain stable equilibrium the plane should be in a vertical direction.