Question

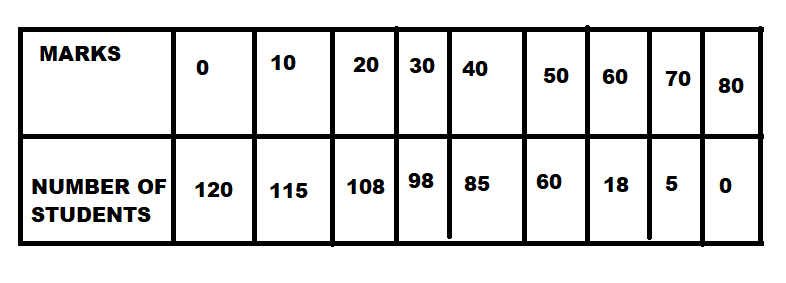
Calculate Karl Pearson’s coefficient of skewness for the following data and interpret the result:

Answer 1

Hint: Here in the given question we need to understand the property of statics, and by using the karl pearson method we can find the related solution, here we need to understand the median, mode and mean, their relation and the associated terms.

Formulae Used:
\[ \Rightarrow \overline x = \dfrac{1}{N}\sum\limits_{i = 1}^n {{f_i} \times {x_i}} \]
\[ \Rightarrow median = \dfrac{{N + 1}}{2}\]
\[ \Rightarrow {S_x} = \dfrac{1}{{N - 1}}\left( {\sum\limits_{i = 1}^n {{f_i} \times {x_i}^2} - \dfrac{{{{\left( {\sum\limits_{i = 1}^n {{f_i} \times {x_i}} } \right)}^2}}}{N}} \right)\]
\[ \Rightarrow {S_x} = \sqrt {{S_x}^2} \]
\[ \Rightarrow {S_k} = \dfrac{{3\left( {Mean - Median} \right)}}{{{S_x} + {S_x}^2}}\]

Complete step by step answer:
Here in the above question, we first need to solve for the required table, with the related quantities, and then solved according on solving we get:

	\[{x_i}\]	\[{f_i}\]	\[{x_i} \times {f_i}\]	\[{x_i}^2 \times {f_i}\]	\[cf\]
	0	120	0	0	120
	10	115	1150	11500	235
	20	108	2160	72000	343
	30	98	2940	88200	441
	40	85	3400	136000	526
	50	60	3000	150000	586
	60	18	1080	64800	604
	70	5	350	24500	609
	80	0	0	0	609
Total	360	649	14080	547000

Now first we need to calculate the mean for the given data:
\[ \Rightarrow \overline x = \dfrac{1}{N}\sum\limits_{i = 1}^n {{f_i} \times {x_i}} \]
Putting the values we get:
\[ \Rightarrow \overline x = \dfrac{1}{N}\sum\limits_{i = 1}^n {{f_i} \times {x_i}} = \dfrac{{14080}}{{649}} = 21.69\]
Here we get the mean marks for each student.
Calculating the median we get:
\[ \Rightarrow median = \dfrac{{N + 1}}{2} = \dfrac{{650}}{2} = 325\]
Here we get the median for the given data.
Now sample variance is given by:
\[
   \Rightarrow {S_x}^2 = \dfrac{1}{{N - 1}}\left( {\sum\limits_{i = 1}^n {{f_i} \times {x_i}^2} - \dfrac{{{{\left( {\sum\limits_{i = 1}^n {{f_i} \times {x_i}} } \right)}^2}}}{N}} \right) \\
   \Rightarrow {S_x}^2 = \dfrac{1}{{649 - 1}}\left( {547000 - \dfrac{{198246400}}{{649}}} \right) = \dfrac{1}{{648}}\left( {547000 - 305464.40} \right) \\
   \Rightarrow {S_x}^2 = \dfrac{1}{{648}}\left( {241535.59} \right) = 372.74 \\
 \]
Now standard deviation is given by:
\[ \Rightarrow {S_x} = \sqrt {{S_x}^2} = \sqrt {372.74} = 19.306\]
Now karl pearson coefficient of skewness is given by:
\[ \Rightarrow {S_k} = \dfrac{{3\left( {Mean - Median} \right)}}{{{S_x} + {S_x}^2}} = \dfrac{{3(21.69 - 325)}}{{19.306 + 372.74}} = \dfrac{{ - 909.93}}{{392.046}} = - 2.3\]
Here we get the negative value for the given data that is less than zero, hence negative skewed.
Note: In the question related to statics we need to find the related terms, as above in order to get the solution for the question, here the table drawn will be different for different types of questions, since every property needs different data in order to get the answer.