
Calculate CFSE of the following complex:
${{\left[ Co{{F}_{6}} \right]}^{3-}}$
(A) −0.4 ${{\Delta }_{o}}$
(B) 0.4 ${{\Delta }_{o}}$
(C) −0.4 ${{\Delta }_{t}}$
(D) 0.6 ${{\Delta }_{t}}$
Answer
585.9k+ views
Hint: The given complex is characterized by a smaller crystal field. As a result, instead of pairing with another electron, electrons choose to occupy the higher d orbitals. From this we can calculate the number of electrons in different orbitals and it will give us the value of CFSE.
Complete step by step solution:
- According to crystal field theory, an octahedral complex which has six ligands systematically arranged around a central atom. Hence, we can assume that the given complex ${{\left[ Co{{F}_{6}} \right]}^{3-}}$is an octahedral complex.
- In an octahedral complex, the d orbitals are split into ${{t}_{2g}}$ and ${{e}_{g}}$.Here the ${{t}_{2g}}$ orbitals will be lower in energy compared to ${{e}_{g}}$orbitals. The splitting can be shown as follows,
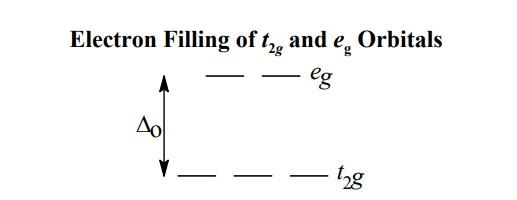
- Let's find the oxidation state of cobalt(x) in ${{\left[ Co{{F}_{6}} \right]}^{3-}}$.We know fluorine has a charge of −1.
$x-6=-3$
∴ $x$=+3
Thus, Co exists as $C{{o}^{3+}}$. Its outer electronic configuration can be given as$3d{{ }^{6}}4{{s}^{0}}$. The arrangement of these 3d electrons will determine the crystal field stabilization energy (CFSE). There are two possible fillings in the ${{t}_{2g}}$ and ${{e}_{g}}$ orbitals for electronic configuration from ${{d}^{4}}$ to ${{d}^{7}}$ .
- There is a high spin configuration which minimizes the pairing of electrons by spreading them across the two orbitals and there is a low spin configuration which minimizes the occupancy of electrons in ${{e}_{g}}$ by the pairing of electrons in ${{t}_{2g}}$itself.
- CFSE of an octahedral complex is given by,
CFSE =$\left( -0.4\times n{{t}_{2g}} \right)+(0.6n{{e}_{g}}){{\Delta }_{o}}$
Where $n{{t}_{2g}}$ is the number of electrons occupied in ${{t}_{2g}}$ orbital and $n{{e}_{g}}$ is the number of electrons occupied in ${{e}_{g}}$ orbital.
- From the spectrochemical series it's clear that ${{F}^{-}}$is a weak field ligand and thus it will give rise to the high spin complex. Therefore, the electrons will spread in both orbitals giving rise to the configuration of ${{t}^{4}}_{2g}{{e}^{2}}_{g}$. This implies that there are four electrons in ${{t}_{2g}}$ orbital and two in ${{e}_{g}}$orbital. Thus, CFSE can be found as follows
CFSE = (−0.4×4) +(0.6×2)
= −1.6+1.2
= −0.4 ${{\Delta }_{o}}$
Therefore, the answer is option (A) −0.4${{\Delta }_{o}}$.
Note: As we mentioned above, the spectrochemical series plays an important role in determining whether the complex is high spin or low spin. It can be represented as follows
${{I}^{-}}<~B{{r}^{-}}<~C{{l}^{-}}<~{{F}^{-}}<~O{{H}^{-}}<~{{C}_{2}}O_{4}^{2-}<~{{H}_{2}}O<~N{{H}_{3}}<~en<~bipy<~phen<~C{{N}^{-}}\approx CO$. Ligands up to water are generally weak ligands and thus form high spin complexes and ligands beyond water are strong field ligands and they form low spin complexes.
Complete step by step solution:
- According to crystal field theory, an octahedral complex which has six ligands systematically arranged around a central atom. Hence, we can assume that the given complex ${{\left[ Co{{F}_{6}} \right]}^{3-}}$is an octahedral complex.
- In an octahedral complex, the d orbitals are split into ${{t}_{2g}}$ and ${{e}_{g}}$.Here the ${{t}_{2g}}$ orbitals will be lower in energy compared to ${{e}_{g}}$orbitals. The splitting can be shown as follows,
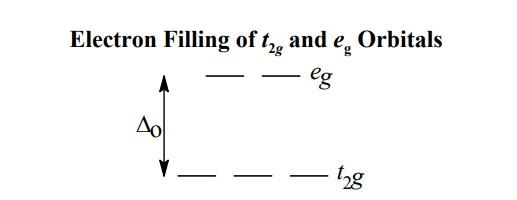
- Let's find the oxidation state of cobalt(x) in ${{\left[ Co{{F}_{6}} \right]}^{3-}}$.We know fluorine has a charge of −1.
$x-6=-3$
∴ $x$=+3
Thus, Co exists as $C{{o}^{3+}}$. Its outer electronic configuration can be given as$3d{{ }^{6}}4{{s}^{0}}$. The arrangement of these 3d electrons will determine the crystal field stabilization energy (CFSE). There are two possible fillings in the ${{t}_{2g}}$ and ${{e}_{g}}$ orbitals for electronic configuration from ${{d}^{4}}$ to ${{d}^{7}}$ .
- There is a high spin configuration which minimizes the pairing of electrons by spreading them across the two orbitals and there is a low spin configuration which minimizes the occupancy of electrons in ${{e}_{g}}$ by the pairing of electrons in ${{t}_{2g}}$itself.
- CFSE of an octahedral complex is given by,
CFSE =$\left( -0.4\times n{{t}_{2g}} \right)+(0.6n{{e}_{g}}){{\Delta }_{o}}$
Where $n{{t}_{2g}}$ is the number of electrons occupied in ${{t}_{2g}}$ orbital and $n{{e}_{g}}$ is the number of electrons occupied in ${{e}_{g}}$ orbital.
- From the spectrochemical series it's clear that ${{F}^{-}}$is a weak field ligand and thus it will give rise to the high spin complex. Therefore, the electrons will spread in both orbitals giving rise to the configuration of ${{t}^{4}}_{2g}{{e}^{2}}_{g}$. This implies that there are four electrons in ${{t}_{2g}}$ orbital and two in ${{e}_{g}}$orbital. Thus, CFSE can be found as follows
CFSE = (−0.4×4) +(0.6×2)
= −1.6+1.2
= −0.4 ${{\Delta }_{o}}$
Therefore, the answer is option (A) −0.4${{\Delta }_{o}}$.
Note: As we mentioned above, the spectrochemical series plays an important role in determining whether the complex is high spin or low spin. It can be represented as follows
${{I}^{-}}<~B{{r}^{-}}<~C{{l}^{-}}<~{{F}^{-}}<~O{{H}^{-}}<~{{C}_{2}}O_{4}^{2-}<~{{H}_{2}}O<~N{{H}_{3}}<~en<~bipy<~phen<~C{{N}^{-}}\approx CO$. Ligands up to water are generally weak ligands and thus form high spin complexes and ligands beyond water are strong field ligands and they form low spin complexes.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




