Question

Calculate area of the figure made by joining \[25\] unit squares
1. \[22\text{ }c{{m}^{2}}\]
2. \[23\text{ }c{{m}^{2}}\]
3. \[24\text{ }c{{m}^{2}}\]
4. \[25\text{ }c{{m}^{2}}\]

Answer 1

Hint: To be able to solve this question first we need to find out what the area of the unit squares will be and why it is the way it is. And then after that once we know the area of any one unit square we can say that the area of all \[25\] of those squares will be the same and hence we can multiply the area we get by \[25\] which will give us the area of the figure that we need for this question.

Complete step-by-step answer:
Now below is depicted how the figure could look if we join \[25\] unit squares together. This is just one of those cases; it doesn’t always have to be like this. For example all of the squares could be arranged and kept together in a horizontal line or a vertical one or many other different cases. This figure just gives us a way to visualize to make the solving easier for us

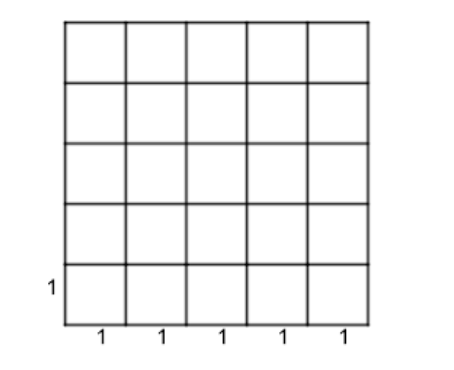
Now it is said to us that those \[25\] squares that we join together are unit squares therefore since it is said to be unit squares we know that the length and breadth of all of the unit squares will be one. Knowing the length and breadth we can find the area
Area of unit square \[=1\times 1=1\text{ }c{{m}^{2}}\]
Now once we know the area of one unit square we can find that the area of the figure where we join all of those \[25\] unit square will be the addition of those \[25\] squares
Area of figure \[=1+1+1....25\text{ }times\]
Therefore area of figure \[25\text{ }c{{m}^{2}}\]
So, the correct answer is “ \[25\text{ }c{{m}^{2}}\]”.

Note: Area can be defined as the space occupied by a flat shape or the surface of an object. Alternatively you can also be given a figure and you can be asked to find the area of shaded parts. In questions like this you just need to divide the shaded parts or the unshaded parts into figures whose areas we can find and therefore by subtraction and addition finding the shaded area.