Question

How do I calculate angle between $ 2 $ vectors ?

Answer 1

Hint: In order to calculate the angle between the $ 2 $ vectors , students should know about the dot product of $ 2 $ vectors. Taking the inverse of the dot product would help us in getting the angle between the $ 2 $ vectors. Before moving on to the dot product, the student should be thorough with the properties of the Vectors, mainly the direction. This is because if the direction of the vector is changed ,its value has to be multiplied by $ - 1 $ . Also the angle between two vectors will be deferred by a single point, which is called the shortest angle at which we will turn around one of the given vectors to the position of co-direction with another vector.

Complete step-by-step answer:
                                                                                

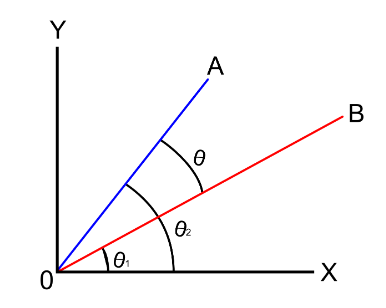
The angle between a vector is always found with respect to positive $ x $ -axis. This will give us the angle between two vectors in standard position. A standard position is the position if it has the initial point origin $ (0,0) $ .
From the above figure , let us define two vectors $ \vec a\& \vec b $ .The dot product between the $ 2 $ vectors is given by $ \vec a.\vec b $ . To know the angle between the vectors we will have to solve the numerical with the formula of dot product.
 $ \vec a.\vec b = |\vec a|.|\vec b|\cos \theta ..........(1) $
To find the angle between the $ 2 $ vectors , we will rearrange the given formula in equation $ 1 $ .
 $ \dfrac{{\vec a.\vec b}}{{|\vec a|.|\vec b|}} = \cos \theta ........(2) $
Theta is the angle between the $ 2 $ vectors. To find the value of $ \theta $ ,we will have to take the inverse of equation $ 2 $ .
 $ \theta = {\cos ^{ - 1}}(\dfrac{{\vec a.\vec b}}{{|\vec a|.|\vec b|}}) $ $ \theta = $

Note: This is just the derivation of the formula, but the sums on this topic would include application of the above formula, for example find the angle between vector \[3\vec i + 4\vec j\]& \[2\vec i - \vec j\]. It is always advised to learn the formula as it will be very helpful in finding the angles and angles between the vectors, length of the vectors.