Question

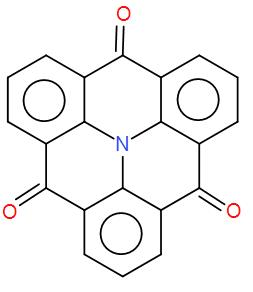
$ {C_3} $ axis of symmetry is not present in this compound.

(A) True
(B) False

Answer 1

Hint: The symmetry of a molecule or a compound is determined by the existence of symmetry operations performed with respect to symmetry elements. A symmetry element is a plane, a line, or a point through an object, about which a reflection or rotation leaves the object in an orientation in an indistinguishable form from the original. A compound has a $ {C_3} $ axis ; when we rotate that compound by 120 degrees, we get the same structure.

Complete Step by step solution:
Symmetry has five types of elements as follows,
Plane of symmetry is a plane of reflection through which an identical copy of the original is produced. Plane of symmetry is also called a mirror plane.
Centre of symmetry or inversion centre: A molecule has a centre of symmetry when any atom in molecule has an identical diametrically centre opposite to it at an equal distance from that molecule that is a molecule has a centre of symmetry when the points x, y, z and -x, -y, -z correspond to identical objects.
Rotation-reflection axis: It is an axis around which a rotation by $ \dfrac{{{{360}^ \circ }}}{n} $ followed by a reflection in a perpendicular plane.
Identify: This symmetry element consists of no change; every molecule has this element. ‘Identify’ is a property that any object should have regardless of its symmetry properties.
Symmetry axis: It is an axis around which rotation $ \dfrac{{{{360}^ \circ }}}{n} $ results in a molecule indistinguishable from the original, it is also called n-fold rotational axis. It is denoted by abbreviated $ {C_n} $ .
So therefore, $ {C_3} $ axis of the above compound will be $ \dfrac{{{{360}^ \circ }}}{3} $ = $ {120^ \circ } $ . The above compound has the $ {C_3} $ axis as when we rotate this compound by 120 degrees, we get the same structure. The $ {C_3} $ axis is present in it which passes through N atom and perpendicular to the plane of the molecule.
Therefore, the statement is false.
The correct answer is option B.

Note
Symmetry of a compound comes under Group Theory. Every molecule possesses one or the other type of symmetry, which also helps us in classifying a molecule. Symmetry helps in the study of molecular orbitals and it helps in applications such as follows:
-Huckel method
-ligand field theory
-Woodward-Hoffmann rules.