Question

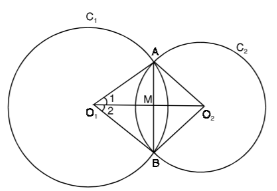
\[{{C}_{1}}\]and \[{{C}_{2}}\] are two circles with center \[{{O}_{1}}\] and \[{{O}_{2}}\] and intersect each other at points \[A\] and \[B\]. If \[{{O}_{1}}{{O}_{2}}\] intersect \[AB\] at \[M\] then show that \[AB\bot {{O}_{1}}{{O}_{2}}\].

Answer 1

Hint: We will try to show \[\Delta {{O}_{1}}AB\]\[\cong \]\[\Delta {{O}_{2}}AB\] using ‘SSS’ type of triangle congruence and then we will show \[\Delta {{O}_{1}}AM\cong \Delta {{O}_{1}}BM\] using ‘SAS’ type of triangle congruence and finally we will show \[AB\bot {{O}_{1}}{{O}_{2}}\]

Complete step by step answer:
Given that two circles \[{{C}_{1}}\] and \[{{C}_{2}}\] with the center \[{{O}_{1}}\] and \[{{O}_{2}}\] intersect each other at points \[A\] and \[B\].
Also, \[{{O}_{1}}{{O}_{2}}\] intersects \[AB\] at \[M\].
Then, we have to show that \[M\] is the midpoint of \[AB\].

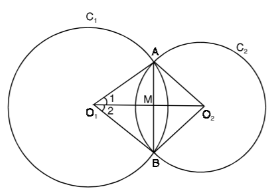
Let us assume that the radius of the circle \[{{C}_{1}}\] be \[r\] and the radius of the circle \[{{C}_{2}}\] be \[s\].
Proof:
In \[\Delta {{O}_{1}}A{{O}_{2}}\] and \[\Delta {{O}_{1}}B{{O}_{2}}\], we have
\[{{O}_{1}}A={{O}_{1}}B.....\left( i \right)\]
Both are radii of the same circle \[{{C}_{1}}\].
\[\Rightarrow {{O}_{2}}A={{O}_{2}}B.....\left( ii \right)\]
Both are radii of the same circle \[{{C}_{2}}\].
Also, \[{{O}_{1}}{{O}_{2}}={{O}_{2}}{{O}_{1}}....\left( iii \right)\]
Common sides of both the triangles \[\Delta {{O}_{1}}A{{O}_{2}}\] and \[\Delta {{O}_{1}}B{{O}_{2}}\]
So, from the equation \[\left( i \right),\left( ii \right)\] and \[\left( iii \right)\], we get both triangles \[\Delta {{O}_{1}}A{{O}_{2}}\] and \[\Delta {{O}_{1}}B{{O}_{2}}\] are congruent with each other by ‘SSS’ type of triangle congruence.
Or, \[\Delta {{O}_{1}}A{{O}_{2}}\cong \Delta {{O}_{1}}B{{O}_{2}}\] by SSS type of triangle congruence.
(Here, ‘SSS’ type means side – side – side type of triangle congruence)
SSS – Theorem

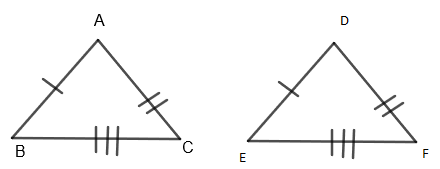
Side-side - side postulate (SSS) states that two triangles are congruent if three sides of one triangle are congruent to the corresponding sides of the other triangle.
Here, from \[\Delta ABC\]and \[\Delta DEF\], we can say that
\[AB=DF....\left( a \right)\]
\[AC=DE....\left( b \right)\]
\[BC=EF....\left( c \right)\]
So, from the equation \[\left( a \right),\left( b \right)\] and \[\left( c \right)\], we have \[\Delta ABC\cong \Delta DEF\] by SSS – type triangle congruence. We can say that ,
\[\Rightarrow M\angle {{O}_{2}}{{O}_{1}}A=M\angle {{O}_{2}}{{O}_{1}}B....\left( iv \right)\] by CPCT
(Here, CPCT is corresponding parts of the congruent triangle)
Also, we have,
\[\Rightarrow M\angle M{{O}_{1}}A=M\angle M{{O}_{1}}B....\left( v \right)\]
From the equation\[\left( iv \right)\], both are the same angles.
 \[\Rightarrow {{O}_{1}}A={{O}_{1}}B.....\left( vi \right)\]by CPCT
Now, in \[\Delta AM{{O}_{1}}\]and \[\Delta BM{{O}_{1}}\], we have
\[\Rightarrow {{O}_{1}}A={{O}_{1}}B....\left( vii \right)\]
(Both are radii of the same circle)
\[\Rightarrow m\angle M{{O}_{1}}A=M\angle M{{O}_{1}}B.....\left( viii \right)\]
From corresponding parts of the congruent triangles.
\[\Rightarrow {{O}_{1}}M=M{{O}_{1}}.....\left( ix \right)\]
Common side of triangles \[\Delta AM{{O}_{1}}\] and \[\Delta BM{{O}_{1}}\].
So, from the equation \[\left( vii \right),\left( viii \right)\] and \[\left( ix \right)\], we get both triangles \[\Delta AM{{O}_{1}}\] and \[\Delta BM{{O}_{1}}\] are congruent with each other by the SAS test of triangle congruence.
Or, \[\Delta AM{{O}_{1}}\cong BM{{O}_{1}}\] by the ’SAS’ test of triangle congruence.
(Here, ‘SAS’ means Side – Angle – Side type of triangle congruence)
SAS – theorem

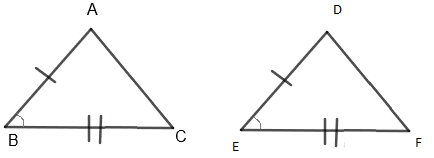
If any two sides and the angle included between those sides for one triangle are equivalent to the corresponding sides and the angle between those sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
Here in the diagram,
Side \[AB=DE\]
Also side \[BC=EF\]
And \[\angle ABC=\angle DEF\]
Thus, \[\Delta ABC\cong \Delta DEF\] by SAS type of triangle congruence.
We can say that,
\[M\angle AM{{O}_{1}}=M\angle BM{{O}_{1}}....\left( x \right)\] by CPCT
(Here CPCT means corresponding part of congruent triangles)
But, \[M\angle AM{{O}_{1}}+M\angle BM{{O}_{1}}=180....\left( xi \right)\]
Because \[M\angle AM{{O}_{1}}\]and \[M\angle BM{{O}_{1}}\] form the linear pair of angles.
Linear pair of angles

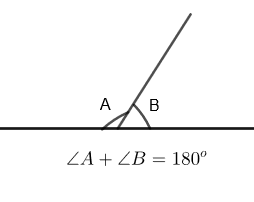
A linear pair is a pair of adjacent supplementary angles. Adjacent means next to each other and supplementary means that the measurement of two angles add up to \[{{180}^{o}}\].
So, from equation \[\left( x \right)\]and \[\left( xi \right)\], we have
\[2M\angle AM{{O}_{1}}=180\]
\[M\angle AM{{O}_{1}}=90\]
Or, \[M\angle AM{{O}_{1}}=M\angle BM{{O}_{1}}=90\]
Both the angles are equal and also they are forming linear pairs.
Therefore, each of the angle is a right angle which clearly shows that
\[AB\bot {{O}_{1}}{{O}_{2}}\]
Hence proved.

Note: Visualize the geometry first before attempting the question. Make a clear diagram of the required question which reduces the probability of error in your solution. We use the SSS and SAS theorems to prove congruence of required triangles and linear pair theorem to prove the required statement.