Question

By vector method, prove that the medians of a triangle are concurrent.

Answer 1

Hint: Median is a line joining a vertex to the midpoint of the opposite side.
The centroid (point of concurrence) divides the
Section Formula: The position vector $ \vec{c} $ of the point C dividing two points A and B with position vectors $ \vec{a} $ and $ \vec{b} $ respectively, in the ratio $ AC:CB=m:n $ internally, is given by $ \vec{c}=\dfrac{n\vec{a}+m\vec{b}}{n+m} $ .
The vector $ \vec{AB} $ from a point A with position vector $ \vec{a} $ to a point B with position vector $ \vec{b} $ , is given by $ \vec{AB}=\vec{b}-\vec{a} $ .
Vectors are added using the Triangle Law of vector addition:
 $ \vec{PQ}+\vec{QR}=\vec{PR} $

Complete step-by-step answer:
Let's say that we have a triangle ABC with AP, BQ and CR as its medians.

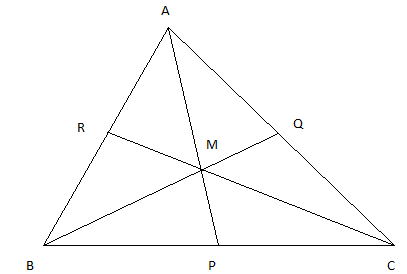
Let's say that the position vectors of the points are:
 $ A=2\vec{a} $
 $ B=2\vec{b} $
 $ C=2\vec{c} $
Using the section formula, the position vectors of the points P, Q and R will be:
 $ P=\dfrac{2\vec{b}+2\vec{c}}{2}=\vec{b}+\vec{c} $
 $ Q=\dfrac{2\vec{a}+2\vec{c}}{2}=\vec{a}+\vec{c} $
 $ R=\dfrac{2\vec{a}+2\vec{b}}{2}=\vec{a}+\vec{b} $
Let's say that the point M divides the vectors $ \vec{AP} $ , $ \vec{BQ} $ and $ \vec{CR} $ in the ratio $ AM:MP=k:1 $ , $ BM:MQ=l:1 $ and $ CM:MR=m:1 $ respectively.
Using the section formula, the position vector of M will be:
 $ \dfrac{k\left( \vec{b}+\vec{c} \right)+2\vec{a}}{k+1} $ OR $ \dfrac{l\left( \vec{a}+\vec{c} \right)+2\vec{b}}{l+1} $ OR $ \dfrac{m\left( \vec{a}+\vec{b} \right)+2\vec{c}}{m+1} $
It can be observed that $ k=l=m=2 $ , satisfy all these three values for the position vector of M.
Therefore, it can be concluded that the three median vectors $ \vec{AP} $ , $ \vec{BQ} $ and $ \vec{CR} $ are concurrent at a point M, which also divides them in the ratio $2:1$ .

Note: The direction of a vector is important: $ \vec{AB}=-\vec{BA} $ .
The position vector $ \vec{c} $ of the mid-point C of two points A and B with position vectors $ \vec{a} $ and $ \vec{b} $ respectively, is given by $ \vec{c}=\dfrac{\vec{a}+\vec{b}}{2} $ .
The vector sum of two or more vectors is also called their resultant. It is the result of adding the vectors together using the triangle law of addition.
The vector component along the x-axis, of a vector $ \vec{r} $ which makes an angle $ \theta $ with the positive direction of the x-axis, is $ |r|\sin \theta $ and the component along the y-axis is $ |r|\cos \theta $ , where $ |r| $ denotes the magnitude of $ \vec{r} $ .