Question

By bending a wire, a square is made whose area is x sq.units. If a circle is made from the same wire, what will be its area?
\[\begin{align}
  & A)\dfrac{11x}{14}sq.unit \\
 & B)\dfrac{12x}{11}sq.unit \\
 & C)\dfrac{14x}{11}sq.unit \\
 & D)\dfrac{11x}{12}sq.unit \\
\end{align}\]

Answer 1

Hint: We know that if a material is changed from one shape to another, then the perimeter of the material is not altered. From the question, it is clear that the square is changed to a circle. So, the perimeter of the square is equal to the circumference of the circle. So, by using this concept, we can find the area of the circle.

Complete step by step answer:
We know that if the side of the square is equal to a, then the area of the square is equal to \[{{a}^{2}}\]. From the question, it is given that the area of the square is equal to x. So, let us assume the side of the square is equal to y.

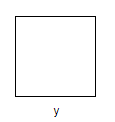
\[\Rightarrow x={{y}^{2}}....(1)\]
Now let us apply square root on both sides, then we get
\[\Rightarrow y=\sqrt{x}....(2)\]
Now, let us find the perimeter of the square. We know that if the side of the square is equal to a, then the perimeter of the square is equal to 4a. From equation (2), we are having the length of the side of the square. So, let us assume the perimeter of the square is equal to z.
So, we get
\[\Rightarrow z=4y....(3)\]
Now we will substitute equation (2) in equation (3), then we get
\[\Rightarrow z=4\sqrt{x}...(4)\]
So, from equation (4), it is clear that the value of z is equal to the perimeter of the square.
We know that if a material is changed from one shape to another, then the perimeter of the material is not altered.
From the question, it is clear that the square is changed to a circle.
So, the perimeter of the square is equal to the circumference of the circle.
We know that the radius of the circle is equal to r, then the circumference of the circle is equal to \[2\pi r\].

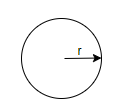
Let us assume the radius of the circle is equal to r and the circumference of the circle is equal to C, then we get
\[\Rightarrow C=2\pi r...(5)\]
We know that the perimeter of the square is equal to the circumference of the circle.
\[\Rightarrow C=z...(6)\]
Now let us substitute equation (4) and equation (5) in equation (6), then we get
\[\Rightarrow 2\pi r=4\sqrt{x}\]
Now by using cross multiplication, then we get
\[\begin{align}
  & \Rightarrow r=\dfrac{4\sqrt{x}}{2\pi } \\
 & \Rightarrow r=\dfrac{2\sqrt{x}}{\pi }....(7) \\
\end{align}\]
We know that the radius of the circle is equal to r, then the area of the circle is equal to \[\pi {{r}^{2}}\].
So, now we should find the area of the circle. Let us assume the area of the circle is equal to A.
\[\Rightarrow A=\pi {{r}^{2}}...(8)\]
Now we should substitute equation (7) in equation (8), then we get
\[\begin{align}
  & \Rightarrow A=\pi {{\left( \dfrac{2\sqrt{x}}{\pi } \right)}^{2}} \\
 & \Rightarrow A=\pi \left( \dfrac{4x}{{{\pi }^{2}}} \right) \\
 & \Rightarrow A=\dfrac{4x}{\pi }....(9) \\
\end{align}\]
We know the value of \[\pi \] is equal to \[\dfrac{22}{7}\].
So, we get
\[\begin{align}
 & \Rightarrow A=\dfrac{28x}{22} \\
 & \Rightarrow A=\dfrac{14x}{11}....(10) \\
\end{align}\]

So, the correct answer is “Option C”.

Note: Students may have a misconception that if a material is changed from one shape to another, then the perimeter of the material is not altered. If this misconception is followed, then we cannot get the correct value of area of the circle. So, this misconception should be avoided. Otherwise, it is impossible to get the correct answer.