Question

How many bricks will be required to construct a wall of 10m long, 6m high and 22.5cm thick, if each brick measures 25cm by 12cm by 9cm?

Answer 1

Hint: The dimensions of a wall is given so on multiplying the length, breadth and height of the wall we will get the volume occupied by the wall in the air as thickness of the wall is given in centimeters (cm) so we have to convert in metres (m) by dividing 22.5 by 100 and we get 0.225m. Now, multiplying length, breadth and the height of the wall we get $10\times 6\times 0.225{{m}^{3}}$. Let us suppose that “n” number of bricks are required to construct a wall so multiply the volume of 1 brick by n and then equate it to the total volume occupied by the wall. Solving this equation will give the number of bricks.

Complete step-by-step answer:

The diagram of a wall given below is:

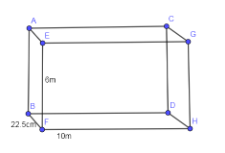
In the above diagram, the length of the wall (FH) is equal to 10m, height of the wall (EF) is equal to 6m and the width of the wall (BF) is 22.5cm.
The diagram of a brick is given below:

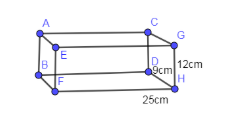
In the above diagram, length of the brick (FH) is equal to 25cm, height of the brick (GH) is equal to 12cm and the width of the brick (DH) is equal to 9cm.
We have given the dimensions of the wall i.e. $10m\times 6m\times 22.5cm$. As the height of the wall is given in cm so we have to convert in metres. To convert 22.5cm into m we are going to divide 22.5 by 100.
$\begin{align}
  & 22.5\left( \dfrac{1}{100} \right) \\
 & =0.225m \\
\end{align}$
The volume of the wall is equal to:
$\begin{align}
  & 10\times 6\times 0.225{{m}^{3}} \\
 & =13.5{{m}^{3}} \\
\end{align}$
We have also given the dimensions of a brick which is $25cm\times 12cm\times 9cm$. As all the units of the dimensions of a brick is in cm so convert into “m”. Converting the unit of dimensions of the brick in “m” we get,
$\begin{align}
  & 25\left( \dfrac{1}{100} \right)\times 12\left( \dfrac{1}{100} \right)\times 9\left( \dfrac{1}{100} \right) \\
 & =0.25\times 0.12\times 0.09{{m}^{3}} \\
 & =0.0027{{m}^{3}} \\
\end{align}$
Now, we are asked to find the number of bricks to construct a wall. Let us assume that “n” number of bricks are required to construct a wall so multiplying the volume of 1 brick by “n” and equate it to the volume of the wall.
$n\times \left( \text{Volume of 1 brick} \right)=\text{Volume of the wall}$
Substituting the volume of 1 brick and the volume of the wall we get,
$\begin{align}
  & n\times 0.0027=13.5 \\
 & \Rightarrow n=\dfrac{13.5}{0.0027} \\
 & \Rightarrow n=5000 \\
\end{align}$
From the above solution, we have found the value of n as 5000.
Hence, 5000 number of bricks required to construct a wall.

Note: You should take care of the units given in the question. In this problem, two places where you have to be careful about the units.
The dimensions of the wall are $10m\times 6m\times 22.5cm$. As you can see that 22.5cm is not in metres so we have to convert in metres.
The dimensions of the brick are $25cm\times 12cm\times 9cm$. As all the dimensions are in “cm” so we have to convert in metres.
We have converted the dimensions of the brick into metres because to find the number of bricks we have equated the volume of n number of bricks to the volume of the wall and as the dimensions of the wall in metres so dimensions of the brick must be in metres.
Don’t forget to write the units of the volume.