Question

How many bricks of 20 cm by 10 cm will be needed to make the floor of a room 25 m long and 16 m wide?

Answer 1

Hint: Apply the area of rectangle formula, to find the area of each brick. Apply the same to find the area of the room. Now divide both the areas to get the number of blocks required. This number is our required result. The area of the rectangle with length l and breadth b is given by the formula, \[Area=l\times b.\]

Complete step-by-step solution:
We know that the area of the rectangle with length l and breadth b is given by the formula, \[Area=l\times b.\]
Area of rectangle = lb

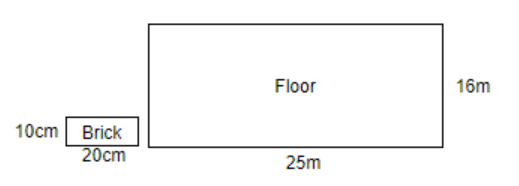
Case 1: Finding the area of brick given in the question. The dimensions of the brick given in the question are written as 20 cm by 10 cm. The length of each brick can be said as,
Length = 20 cm …..(i)
From the dimensions, we can say the breadth of the brick as,
Breadth = 10 cm…..(ii)
By multiplying (i) and (ii), we get,
\[\text{Length}\times \text{Breadth}=20cm\times 10cm\]
By using the formula of area, we can write this as,
Area of each brick = \[20cm\times 10cm\]
By simplifying the above equation, we can write it as,
Area of each brick \[=200c{{m}^{2}}\]
Case 2: Finding the area of the room given in the question. The dimensions of the room are given in the form of 25m long and 16m wide. We know the relation between the units m and cm as 1m = 100 cm.
By multiplying 25 on both the sides, we get the relation as 25m = 2500 cm.
By multiplying 16 and dividing 25 on both the sides, we get the relation as 16m = 1600 cm.
By using the above relation, we can say that length of the room is l = 25m = 2500 cm.
By using the above relation, we can say that the breadth of the room is b = 16m = 1600 cm.
By multiplying the above equations, we can write the equation as,
\[l\times b=2500\times 1600\]
By using the formula of the area, we can write it as,
\[A=40,00,000c{{m}^{2}}\]
Let us assume k bricks of \[A=200c{{m}^{2}}\] needed to fill an area of \[40,00,000c{{m}^{2}}.\] By the above assumption, we can write the equation in the form,
\[200\times k=40,00,000\]
By dividing with 200 on both the sides, we can write it as,
\[k=\dfrac{40,00,000}{200}=20,000\text{ bricks}\]
Therefore, we need 20,000 bricks to make the floor of the room.

Note: Students forget to change the units and divide directly, then they get 2 bricks. But the area of the room is in \[{{m}^{2}},\] and area of the brick is in \[c{{m}^{2}}.\] Alternatively, you can find the area of the room in \[{{m}^{2}}\] and then convert it to \[c{{m}^{2}}.\] Anyways you will get the same result. Be careful while using the relation between the two areas obtained in terms of k.