Question

Both the springs are identical and the friction is absent everywhere. Both the systems will be in equilibrium.

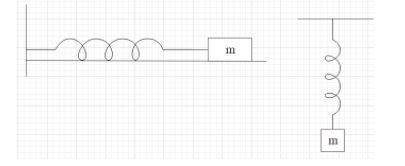
When we displace this thing,
A. Time period for both the simple harmonic motion will be the same
B. Time period for the vertical simple harmonic motion will be larger
C. If both the blocks were displaced by the similar amount from the respective equilibrium. Therefore the amplitude of the oscillators will be identical.
D. none of these

Answer 1

Hint: The time period of the system can be found by taking the product of the twice the value of pi and the square root of the ratio of the mass of the block to the spring constant. As the mass of the block and spring constant of the spring are mentioned, compare both the situations and find out the time period of both the conditions. This will help you in answering this question.

Complete step-by-step answer:
as we already mentioned in the question the springs are found to be identical and the friction will be absent everywhere, therefore the spring constant for both the springs will be identical. And also we can see that the mass of the blocks in both the conditions are mentioned to be the same. Therefore we can write that,
The time period of the system can be found by taking the product of twice the value of pi and the square root of the ratio of the mass of the block to the spring constant. Therefore we can write that,
$T=2\pi \sqrt{\dfrac{m}{k}}$
Where $m$ be the mass of the block and $k$ be the spring constant of the spring.
As the mass and the spring constant are identical, the time period will also be identical. Therefore the time period of both the situations will be the same.

So, the correct answer is “Option A”.

Note: The time period is defined as the time taken using a complete cycle of the wave in order to pass a point. The time period can be found by taking the reciprocal of the frequency of the wave. Frequency is defined as the number of complete cycles of waves which is passing a position in unit time.