Question

Bong walks $ 100 $ m due North and then $ 150 $ m in a direction N $ {37^ \circ } $ E. How far is Bong from his original position?

Answer 1

Hint: We are given that there is a person Bong who walks $ 100 $ m in the North direction and then turns $ {37^ \circ } $ towards East and walks $ 150 $ m. We have to find how far he currently is from the starting point. In this question, first try to draw a rough diagram to get the proper idea of what we have to calculate and then try to apply the Law of Cosines i.e.,
 $
  {a^2} = {b^2} + {c^2} - 2bc\cos A \\
  {b^2} = {a^2} + {c^2} - 2ac\cos B \\
  {c^2} = {a^2} + {b^2} - 2ab\cos C \;
  $

Complete step by step solution:
(i)
According to the given information in the question, we will first draw a rough diagram describing the route Bong took while walking.
So, first we will mark the starting point as A. Then he walked $ 100 $ m in the North and reached a point we will name as B. Then he turned $ {37^ \circ } $ towards East and walked $ 150 $ m and reached his final destination which we will name as C.

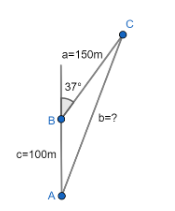
So, this is the diagram we obtained.
(ii)
In the drawn diagram we have a triangle $ \vartriangle ABC $ whose sides are as follows:
 $
  a = 150 \\
  c = 100 \;
  $
And $ b $ is unknown. In order to obtain the length of side $ b $ , we will apply the law of cosines.
 $
  {a^2} = {b^2} + {c^2} - 2bc\cos A \\
  {b^2} = {a^2} + {c^2} - 2ac\cos B \\
  {c^2} = {a^2} + {b^2} - 2ab\cos C \;
  $
Since, we want the value of $ b $ , we will use the second formula i.e.,
 $ {b^2} = {a^2} + {c^2} - 2ac\cos B $
We know that $ a = 150 $ , $ c = 100 $ and $ \angle B = 180 - 37 = {143^ \circ } $
So, putting the values in the formula $ {b^2} = {a^2} + {c^2} - 2ac\cos B $ we will get:
 $ {b^2} = {\left( {150} \right)^2} + {\left( {100} \right)^2} - 2\left( {150} \right)\left( {100} \right)\cos 143 $
(iii)
Solving the above equation, we will get:
 $
  {b^2} = 22500 + 10000 - 30000\left( { - 0.798} \right) \\
  {b^2} = 22500 + 10000 + 23940 \\
  {b^2} = 56440 \\
  b = \sqrt {56440} \\
  b = 237.571 \;
  $
Since, $ b $ is the shortest distance from the starting point to the final destination, we can say that Bong is $ 237.571 $ m away from his original position.
So, the correct answer is “ $ 237.571 m $ ”.

Note: While drawing the diagram, we need to keep in mind that we are mentioning the correct directions and that $ {37^ \circ } $ turn is from the vertical line. But, $ \angle B $ here is the inner angle of the triangle and thus, we needed to subtract $ {37^ \circ } $ from $ 180 $ in order to find $ \angle B $ . In the calculation, we need to be careful to prevent small mistakes.