Question

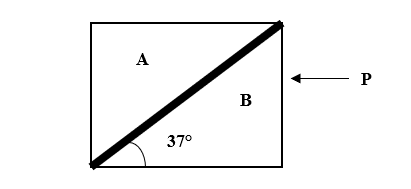
Blocks A and B each have the same mass m= 1 kg. The largest horizontal force P (in Newton) which can be applied to B so that A will not slip up on B. Find the value of P. (Neglect any friction)

A.16 N
B.5 N
C.25 N
D.15 N

Answer 1

Hint: Upward force should be equal to the downward force so that the block A does not slip on block B. So, first find the upward force on block A and then the downward force on block A. Then equate these two forces. Substitute the values in the equation and find the value of P. This will give the largest horizontal force applied to block B so that block A will not slip up on block B.

Complete answer:

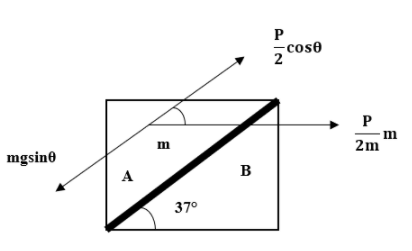
Given= ${\theta} = 37°$
             Mass of both the blocks (m)= 1 kg
For the block A to not slip on block B, the upward force should be equal to the downward force.
Upward force is given by,
${F}_{up}= \dfrac {P}{2}\cos {\theta}$
Downward force is given by,
${F}_{down} =mg \sin {\theta}$
For A to not slip up on B,
${F}_{up}={F}_{down}$
Substituting the values in above equation we get,
$\dfrac {P}{2}\cos {\theta}= mg \sin {\theta}$
Rearranging the above equation we get,
$P= 2mg \tan {\theta}$
Substituting the values in above equation we get,
$P= 2 \times 10 \tan {37°}$
$\Rightarrow P= 20 \times 0.75$
$\Rightarrow P= 15N$
Hence, the largest horizontal force of 15N can be applied to B so that A will not slip on B.

So, the correct answer is option D i.e. 15N.

Note:
Students must take care that they do not consider friction while solving the problem as it is clearly mentioned in the question. If we consider the friction, the answer would change and it might not match the given options. Students must take care while writing the sine and cosine components of any parameter.