Question

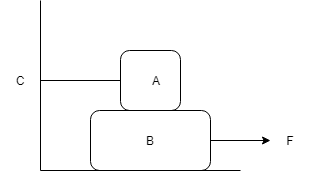
Block A of weight 100 kg rests on block B and is tied with a horizontal string to the wall at C. Block B weights 200 kg. The coefficients of friction between A and B are 0.25 and between B and surface is $\dfrac{1}{3}$ The horizontal force $F$ necessary to move the block B should be ($g=10m{s^{ - 2}}$)

A) 1150 N
B) 1250 N
C) 1300 N
D) 1420 N

Answer 1

Hint: The horizontal force needed to move block B can easily be calculated by the formula of calculating frictional force which says that f=$\mu N$, $f$ is the frictional force, $\mu $ is the coefficient of friction and $N$ is the normal force which is the product of mass and acceleration. In moving B we will calculate force for A and then for B separately then add it for final force $F={\mu _{AB}}$mg + ${\mu _{BS}}$$\left( {{m_A} + {m_B}} \right)$g.

Complete Step by Step Answer:
Let a loaded truck with a mass (\[{m_{truck}}\]) be travelling at the velocity (\[{v_{truck}}\]).

Step 1:
The coefficient of friction is defined as the ratio of the force required to move two sliding surfaces over each other, and the force holding them together.
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other.
There are several types of friction: Dry friction is a force that opposes the relative lateral motion of two solid surfaces in contact.
And Coefficient of friction is given by $f=\mu N$ ….. (1),
Here $f$ is the frictional force, $\mu $ is the coefficient of friction and $N$ is the normal force which is the product of mass and acceleration.

Step 2:
Here in the question we will use acceleration due to gravity $g=10m{s^{ - 2}}$
We are given in the question and the diagram that a block $A$ is there of mass $100kg={m_A}$
And it rests on another block B of mass $200kg={m_B}$
The coefficients of friction between A and B are $0.25={\mu _{AB}}$
And the coefficients of friction between B and surface is $\dfrac{1}{3}$=${\mu _{BS}}$
Gravity is given $10m{s^{ - 2}}$
Now, using equation (1) Coefficient of friction is given by f=$\mu N$
$f$ is the frictional force, $\mu $ is the coefficient of friction and $N$ is the normal force which is the product of mass and acceleration.
So we can write it as $f= \mu \left( {mg} \right)$ ….. (2)
Force for A and B will be f=${\mu _{AB}}$mg ….. (3)
And force for B and surface will be =${\mu _{BS}}$$\left( {{m_A} + {m_B}} \right)$g …… (4),
because box A lies on box B which increases the weight.
Total force will be the addition of equation (3) and (4)
This will give
$F={\mu _{AB}}$mg + ${\mu _{BS}}$$\left( {{m_A} + {m_B}} \right)$g
Substituting the values we get,
$F=0.25 \times 100 \times 10 + \dfrac{1}{3} \times (100+200) \times 10$
On solving the above equation we will get
$F=1250 N$

$\therefore$ The horizontal force F necessary to move the block B should be 1250 N. Option B is correct.

Note:
We need to add the mass of block A in calculating force acting on block B and surface. The reason is when we are calculating frictional force for A we only have to consider its coefficient and mass but at the time for B the mass becomes more as A lies on it so the force will change accordingly.