Question

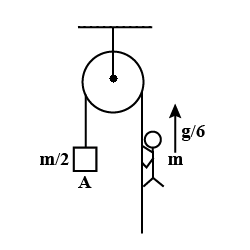
Block A of mass m/2 is connected to one end of light rope which passes over a pulley as shown in the figure. Man of mass m climbs the other end of rope with a relative acceleration of g/6 with respect to rope. Find acceleration of block A and tension in the rope.

Answer 1

Hint: At first we need to draw the diagram which will represent in which direction there is tension in the rope, Now after that we need to draw the free body diagram of the man considering the man as a point mass. From that free body diagram we can form the equation of net force with which we will get the tension in the rope. Now we have to draw the free body diagram of the block and compare the acceleration with which the block is going downwards to the tension in the string, in this way we will get the direction in which acceleration is going to take place, now again write the equation of net force and find the acceleration of the block.

Complete step by step answer:
From the question we get to know that, mass of the man is m.
The mass of the block A is m/2.
The man is climbing the rope with relative acceleration of g/6 with the rope.

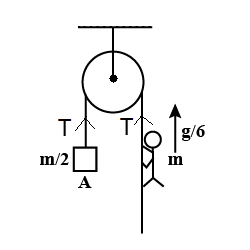
Now, in the above diagram we can see that, as the rope is the same , tension T is acting on both sides of the pulley.
Now, if we take the man as a point mass then,

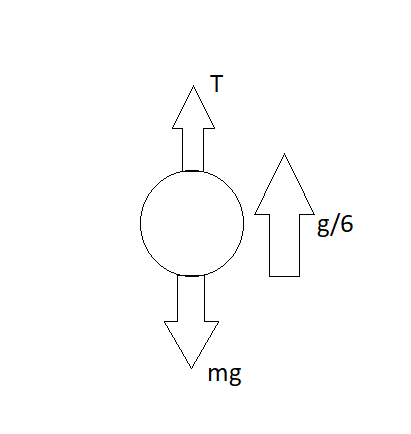
Here, we see that the man is considered as a point mass and the rope he is holding has a tension of T, and the man is also accelerating with an acceleration of g/6. And as the man is hanging so the mass of the man will act downwards with the acceleration of gravity that is mg.
Now, we are going to apply Newton’s second law of motion,
So,
$T-mg=m\times \dfrac{g}{6}$ ,
So, from here we can find the tension in the rope so,
$T=\dfrac{7mg}{6}$So, this is the tension in the rope. This is one of the answers.
Now, the question wants to know that, what is the acceleration of block A.
So,
We will now draw the free body diagram of the block A,

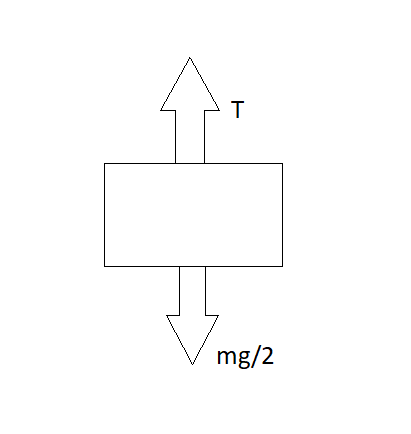
Here we can see that the block A is pulled up with a tension of T, and a mass of mg/2 is acting downwards due to the mass of the block.
Now, we know the tension of the rope that is, $T=\dfrac{7mg}{6}$, and thus we can see by comparing the downward acceleration and upward acceleration that the tension T is greater than the downward acceleration.

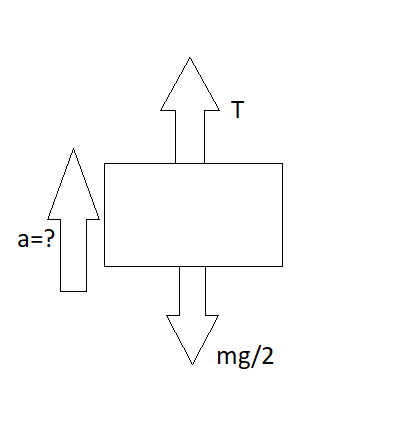
So the block will go up and we will have to find the acceleration with which it will go upwards,
So, now again we will apply Newton’s second law of motion, and find the net force,
$\dfrac{7mg}{6}-\dfrac{mg}{2}=\dfrac{m}{2}\times a$ ,
On solving we will get acceleration a of the block as,
$a=\dfrac{4g}{3}$ .
So, the tension in the rope is $T=\dfrac{7mg}{6}$ and the acceleration of the block A is $a=\dfrac{4g}{3}$ in upward direction.

Note: Students must take care that the rope is the same as the tension acting on the rope will be in the same direction. The direction of acceleration for the block is necessary as then only we can understand in which direction we will have to calculate the acceleration.