
BL and CM are medians of the given triangle ABC right angled at A.
Prove that \[4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}}\].
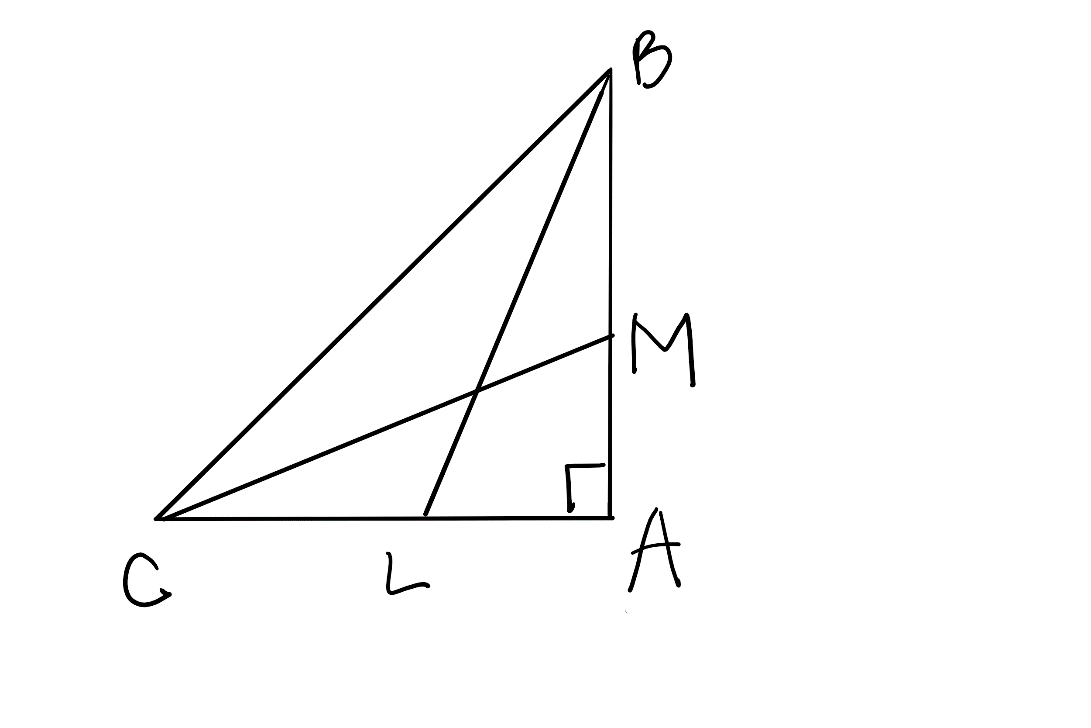
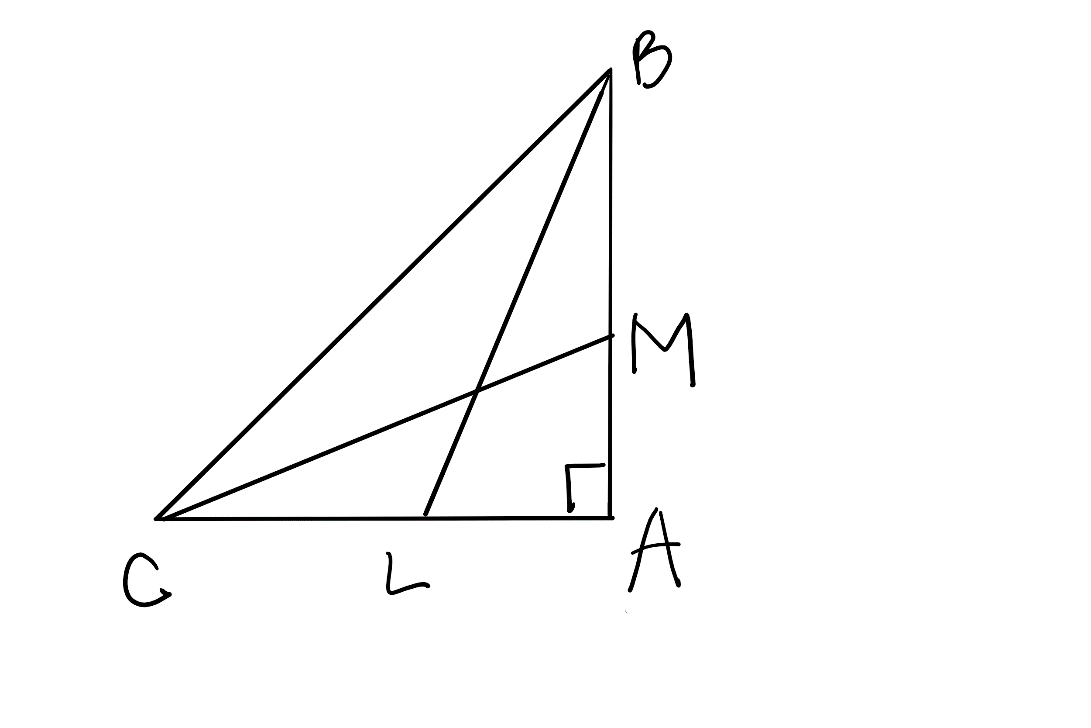
Answer
607.8k+ views
- Hint: To solve this question we will use the fact that the median of the line divides the line in two equal parts. Also, will use Pythagoras theorem stated as “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.”
Complete step-by-step solution -
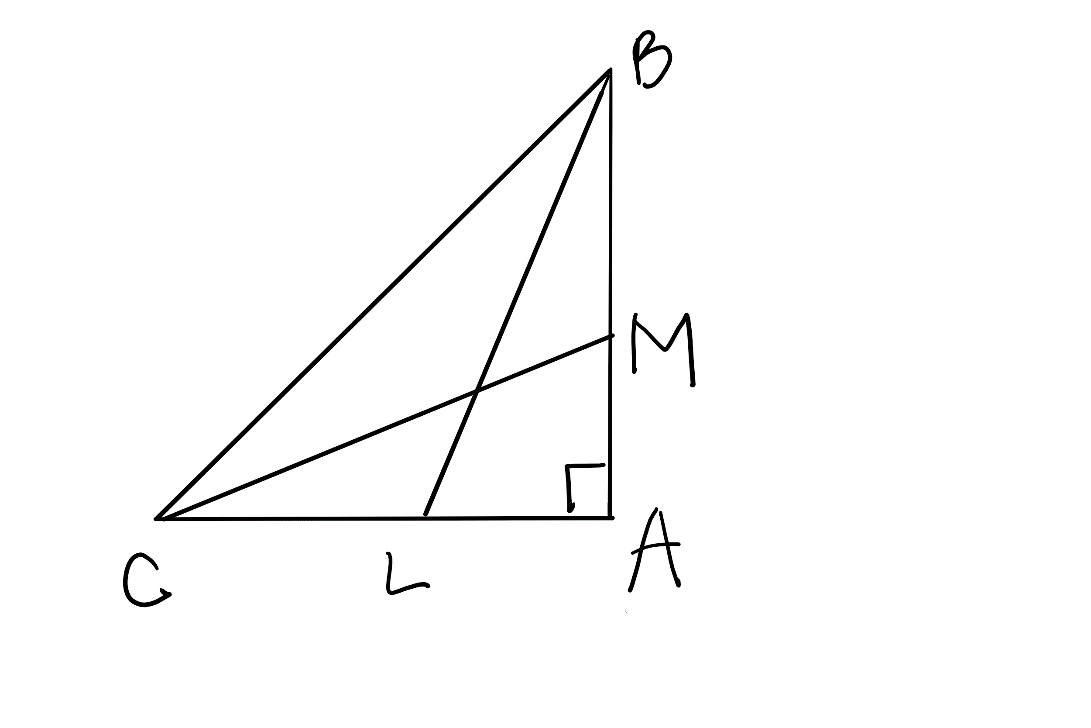
Given that BL and CM are medians of the given triangle ABC right angled at A.
To prove \[4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}}\].
Since BL is the Median of the line AC of the triangle ABC, so it cuts the line AC into two parts.
Therefore,
\[AL=CL=\dfrac{1}{2}AC\text{ }.......\text{ }\left( i \right)\]
Again, similarly since CM is the Median of the line AB of the triangle ABC, so it cuts the line AB into two parts.
Therefore,
\[AM=MB=\dfrac{1}{2}AB\text{ }.......\text{ }\left( ii \right)\]
As the triangle ABC is a right-angled triangle.
Therefore, applying Pythagoras theorem in the triangle ABC which is stated as,
In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
\[B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}........(iii)\]
Similarly, the triangle BAL is a right-angled triangle.
Applying Pythagoras theorem to it we get,
\[B{{L}^{2}}=A{{B}^{2}}+A{{L}^{2}}\].
Substituting the value of AL from equation (i) we get,
\[\begin{align}
& B{{L}^{2}}=A{{B}^{2}}+{{(\dfrac{1}{2}AC)}^{2}} \\
& \Rightarrow B{{L}^{2}}=A{{B}^{2}}+\dfrac{1}{4}A{{C}^{2}} \\
& \Rightarrow 4B{{L}^{2}}=4A{{B}^{2}}+A{{C}^{2}}........(iv) \\
\end{align}\]
Again, similarly applying the same in triangle MAC, we have,
\[C{{M}^{2}}=A{{C}^{2}}+A{{M}^{2}}\]
Substituting the value of AM from equation(ii) we get,
\[\begin{align}
& C{{M}^{2}}=A{{C}^{2}}+{{(\dfrac{1}{2}AB)}^{2}} \\
& \Rightarrow C{{M}^{2}}=A{{C}^{2}}+\dfrac{1}{4}A{{B}^{2}} \\
& \Rightarrow 4C{{M}^{2}}=4A{{C}^{2}}+A{{B}^{2}}.........(v) \\
\end{align}\]
Now adding equation (iv) and equation(v) we get,
\[\begin{align}
& 4B{{L}^{2}}+4C{{M}^{2}}=4A{{B}^{2}}+A{{C}^{2}}+4A{{C}^{2}}+A{{B}^{2}} \\
& \Rightarrow 4(B{{L}^{2}}+C{{M}^{2}})=5A{{B}^{2}}+5A{{C}^{2}} \\
& \Rightarrow 4(B{{L}^{2}}+C{{M}^{2}})=5(A{{B}^{2}}+A{{C}^{2}}) \\
\end{align}\]
Now using the equation(iii) in the right-hand side of the above obtained equation we get,
\[\begin{align}
& 4(B{{L}^{2}}+C{{M}^{2}})=5(A{{B}^{2}}+A{{C}^{2}}) \\
& \Rightarrow 4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}} \\
\end{align}\]
Therefore, we obtained the required expression, that is, \[4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}}\].
Hence proved.
Note: The possibility of error in these types of questions could be not assuming equation numbers which can lead to confusions and hence wrong result at the end. Always assume equation numbers and use them accordingly.
Complete step-by-step solution -
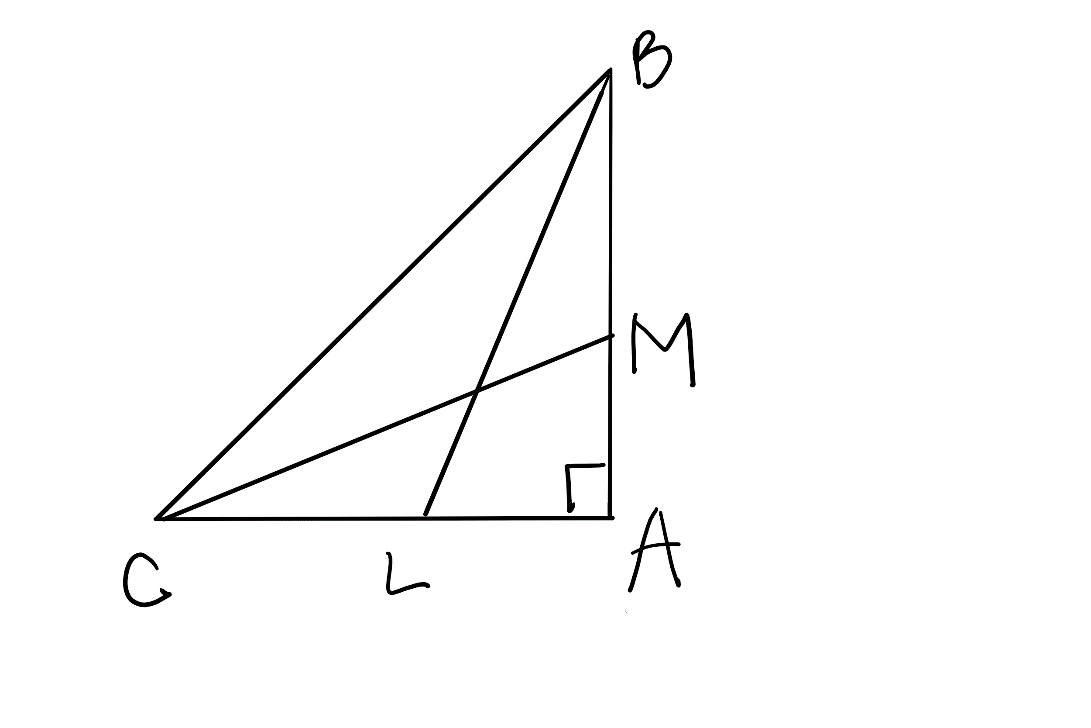
Given that BL and CM are medians of the given triangle ABC right angled at A.
To prove \[4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}}\].
Since BL is the Median of the line AC of the triangle ABC, so it cuts the line AC into two parts.
Therefore,
\[AL=CL=\dfrac{1}{2}AC\text{ }.......\text{ }\left( i \right)\]
Again, similarly since CM is the Median of the line AB of the triangle ABC, so it cuts the line AB into two parts.
Therefore,
\[AM=MB=\dfrac{1}{2}AB\text{ }.......\text{ }\left( ii \right)\]
As the triangle ABC is a right-angled triangle.
Therefore, applying Pythagoras theorem in the triangle ABC which is stated as,
In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
\[B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}........(iii)\]
Similarly, the triangle BAL is a right-angled triangle.
Applying Pythagoras theorem to it we get,
\[B{{L}^{2}}=A{{B}^{2}}+A{{L}^{2}}\].
Substituting the value of AL from equation (i) we get,
\[\begin{align}
& B{{L}^{2}}=A{{B}^{2}}+{{(\dfrac{1}{2}AC)}^{2}} \\
& \Rightarrow B{{L}^{2}}=A{{B}^{2}}+\dfrac{1}{4}A{{C}^{2}} \\
& \Rightarrow 4B{{L}^{2}}=4A{{B}^{2}}+A{{C}^{2}}........(iv) \\
\end{align}\]
Again, similarly applying the same in triangle MAC, we have,
\[C{{M}^{2}}=A{{C}^{2}}+A{{M}^{2}}\]
Substituting the value of AM from equation(ii) we get,
\[\begin{align}
& C{{M}^{2}}=A{{C}^{2}}+{{(\dfrac{1}{2}AB)}^{2}} \\
& \Rightarrow C{{M}^{2}}=A{{C}^{2}}+\dfrac{1}{4}A{{B}^{2}} \\
& \Rightarrow 4C{{M}^{2}}=4A{{C}^{2}}+A{{B}^{2}}.........(v) \\
\end{align}\]
Now adding equation (iv) and equation(v) we get,
\[\begin{align}
& 4B{{L}^{2}}+4C{{M}^{2}}=4A{{B}^{2}}+A{{C}^{2}}+4A{{C}^{2}}+A{{B}^{2}} \\
& \Rightarrow 4(B{{L}^{2}}+C{{M}^{2}})=5A{{B}^{2}}+5A{{C}^{2}} \\
& \Rightarrow 4(B{{L}^{2}}+C{{M}^{2}})=5(A{{B}^{2}}+A{{C}^{2}}) \\
\end{align}\]
Now using the equation(iii) in the right-hand side of the above obtained equation we get,
\[\begin{align}
& 4(B{{L}^{2}}+C{{M}^{2}})=5(A{{B}^{2}}+A{{C}^{2}}) \\
& \Rightarrow 4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}} \\
\end{align}\]
Therefore, we obtained the required expression, that is, \[4(B{{L}^{2}}+C{{M}^{2}})=5B{{C}^{2}}\].
Hence proved.
Note: The possibility of error in these types of questions could be not assuming equation numbers which can lead to confusions and hence wrong result at the end. Always assume equation numbers and use them accordingly.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Which Country is Called "The Land of Festivals"?

What type of cell is found in the Seminiferous tub class 10 biology CBSE

What are the public facilities provided by the government? Also explain each facility




