Question

BC is given. Construct $\angle ABC$, $\angle PBC$ and $\angle QBC$ such that m $\angle ABC = {60^\circ }$, m $\angle PBC = {30^ \circ }$ and m $\angle QBC = {15^\circ }$ with the help of a pair of compass and straight edge. Write the steps of construction.

Answer 1

Hint: First draw an arc from point B at point M. Then again make an arc from point M that passes through B and intersects the previously drawn arc at point A. Join the line AB. This will give use $\angle ABC = {60^\circ }$. Now we have to make $\angle PBC = {30^ \circ }$ by drawing an angle bisector of the already drawn $\angle ABC = {60^\circ }$. To draw $\angle QBC = {15^\circ }$, draw angle bisector of $\angle PBC = {30^ \circ }$.

Complete step-by-step answer:
We have to construct $\angle ABC$, $\angle PBC$, and $\angle QBC$ on the given line BC. The measure of angles is given as- $\angle ABC = {60^\circ }$, $\angle PBC = {30^ \circ }$ and $\angle QBC = {15^\circ }$
Steps of construction:
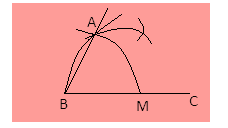
Step 1- First take the compass and open it to a convenient radius. Place its pointer at B and with a pencil-head make an arc that will meet the line BC at point M.

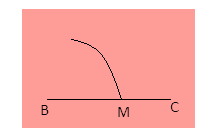
Step 2- Place the compass pointer at point M and mark an arc that passes through B and intersects the drawn previously at point A.
Step 3- Draw a line from point B to A.

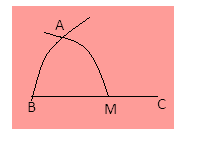
Step 3- Draw a line from point B to A.

We get the required$\angle ABC = {60^\circ }$.
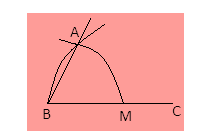
Step 4- Now place the compass pointer at M and draw the arc above M that passes through A. Then placing the compass pointer at A, draw an arc across the previously drawn arc.

Step 5- Now join BP.

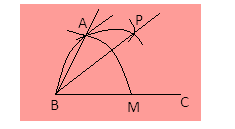
We get the required angle $\angle PBC = {30^ \circ }$
Step 6- To draw angle$\angle QBC = {15^\circ }$ we will draw the angle bisector of $\angle PBC = {30^ \circ }$which divides the angle into two halves.
Name the point N where the arc from M intersects line PB.
Now, draw an arc from Point M and Point N respectively and the point of their intersection is Q.

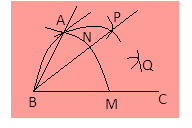
Step 7- Now, join line QB.

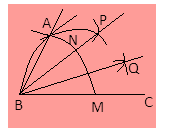
We get the required $\angle QBC = {15^\circ }$.
Note: Here the straight edge means ruler. We have not used a protractor to draw the angle given because in the question it is written that we have to draw the angle using a compass and ruler only.
In the given question we could have drawn $\angle PBC = {30^ \circ }$ by bisecting the angle $\angle ABC = {60^\circ }$as we did while drawing angle $\angle QBC = {15^\circ }$. We could also draw $\angle PBC = {30^ \circ }$ by creating a rhombus PABM and its diagonal PB would give us the angle $\angle PBC = {30^ \circ }$.