Question

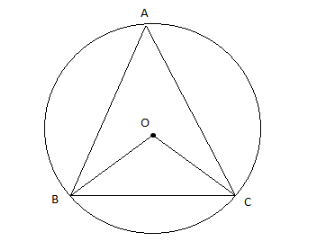
BC is a chord of a circle with center O. If A is a point on the major arc BC as shown in the figure, then $ \angle BAC+\angle OBC=\_\_\_\_\_\_ $ ?

A. $ 45{}^\circ $
B. $ 90{}^\circ $
C. $ 180{}^\circ $
D. $ 165{}^\circ $

Answer 1

Hint: The radii of a circle are equal, therefore $ \Delta BOC $ is isosceles and $ \angle OBC=\angle OCB $ .
The angle subtended by two fixed points at the center is double the angle subtended by them at any point on the major arc of the circle.
In other words, $ \angle BOC=2\angle BAC $ .
Assume that $ \angle BAC=x{}^\circ $ , then how much will be the $ \angle OBC $ in terms of $ x $ ?

Complete step-by-step answer:
From the properties of the angles subtended by an arc, we know that $ \angle BOC=2\angle BAC $ .
Let's say that $ \angle BAC=x{}^\circ $ .
Therefore, $ \angle BOC=2x{}^\circ $ .
Now, in the triangle $ \Delta BOC $ , $ OB=OC $ (radius), therefore, $ \angle OBC=\angle OCB=y{}^\circ $ (say).
We know that the sum of the angles of a triangle is $ 180{}^\circ $ .
∴ $ \angle BOC+\angle OBC+\angle OCB=180{}^\circ $
⇒ $ 2x{}^\circ +y{}^\circ +y{}^\circ =180{}^\circ $
⇒ $ 2x{}^\circ +2y{}^\circ =180{}^\circ $
On dividing LHS and RHS by 2; we get
⇒ $ x{}^\circ +y{}^\circ =90{}^\circ $
Also, $ \angle BAC=x{}^\circ $ (assumed) and $ \angle OBC=y{}^\circ $ (assumed).
∴ $ \angle BAC+\angle OBC=90{}^\circ $ .
The correct answer is B. $ 90{}^\circ $ .
So, the correct answer is “Option B”.

Note: Chords of circle which are equal in length, also subtend equal angles at the center.
The angles subtended by a chord in the major and the minor arc add up to $ 180{}^\circ $ .
The angle subtended by the diameter on any point on the circle is always $ 90{}^\circ $ and called as angle in semicircle.
The longest chord of a circle is the diameter of the circle.