Question

What is the basic unit by which angles are measured?

Answer 1

Hint: There are two basic units by which angles are measured. From one of the two basic units- one is degree $\left( ^{\circ } \right)$ and other is radians $\left( \pi \right)$. Now, the full angle of a circle starting from any point and then moving in the counterclockwise direction from this point will make the angle of ${{360}^{\circ }}$. And there is a relation between degree and radians which we are going to explain in the below.

Complete step by step solution:
In the below, we are showing a diagram which is showing the angle between two line segments.

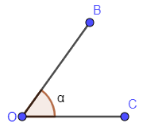
From the above figure, COB is the angle with a value of $\alpha $.
Now, in the above problem, we are asked to find the unit of this angle so there are two basic units of measuring this angle and they are as follows:
Degree $\left( ^{\circ } \right)$ and radians $\left( \pi \right)$.
In a circle, the complete angle is of measurement of ${{360}^{\circ }}$ and in the figure below we are showing a circle with complete angle ${{360}^{\circ }}$.

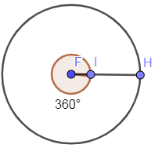
In this figure, the circle drawn with brown color is the full angle ${{360}^{\circ }}$ and this angle is drawn from point I in the counterclockwise direction so that we again reach point I.
Now, there is a relation between $\pi $ and degree which is as follows:
$2\pi \to {{360}^{\circ }}$
So, from the above relation we can oscillate from one basic unit to another.

So, we can also write the full angle that can be made on the centre of the circle as $2\pi $.

Note:
In the below, we have shown that how to convert radians into degree:
$2\pi \to {{360}^{\circ }}$
Now, 1 radian is found by dividing $2\pi $ on both the sides of the above and we get,
$1\to \dfrac{{{360}^{\circ }}}{2\pi }$
Similarly, we can convert degree into radian in the following way:
${{360}^{\circ }}\to 2\pi $
Now, dividing ${{360}^{\circ }}$ on both the sides and we get,
${{1}^{\circ }}\to \dfrac{2\pi }{{{360}^{\circ }}}$