Question

Ball A is dropped from the top of a building. At the same instant ball B is thrown vertically upwards from the ground. When the balls collide, they are moving in opposite directions and the speed of A is twice the speed of B. At what fraction of the height of the building did the collision occur?
A. $\dfrac{1}{3}$
B. $\dfrac{2}{3}$
C. $\dfrac{1}{4}$
D. $\dfrac{2}{5}$

Answer 1

Hint: Here we have two balls, one dropped from the top of a building and other thrown from ground. These balls collide at a particular time at a particular height. By using the kinematic equations for both the balls, we will get the solution.

Formula used: ${{s}_{A}}={{u}_{A}}t+\dfrac{1}{2}g{{t}^{2}}$
${{v}^{2}}-{{u}^{2}}=2as$

Complete step by step answer:
In the question it is said that a ball ‘A’ is dropped from the top of a building and at the same time a ball ‘B’ is thrown vertically upwards from the ground.
The balls collide after a time and the speed of the ball ‘A’ becomes twice the speed of the bll ‘B.
The figure below shows the given situation.

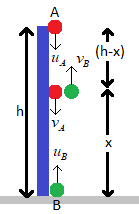
Here ‘${{u}_{A}}$’ and ‘${{u}_{B}}$’ are the initial velocities of the balls A and B respectively and ‘${{v}_{A}}$’ and ‘${{v}_{B}}$’ are the final velocities of the balls A and b respectively.
Since after collision the speed of ball A is twice the speed of ball B, we can say that,
${{v}_{A}}=2{{v}_{B}}$
Let ‘x’ be the height from the ground where the collision occurs and ‘h’ be the total height of the building. Then we have the height from the top of the building to the site where collision occurs as,
$\left( h-x \right)$
From the second equation of motion, we have
$s=ut+\dfrac{1}{2}a{{t}^{2}}$, were ‘s’ is the displacement, ‘u’ is the initial velocity, ‘t’ is the time taken and ‘a’ is the acceleration.
By applying this equation for ball A, we get
$\Rightarrow {{s}_{A}}={{u}_{A}}t+\dfrac{1}{2}g{{t}^{2}}$
We know that the displacement of the ball A is $\left( h-x \right)$ and the initial velocity of the ball A is zero.
Thus we get,
$\Rightarrow \left( h-x \right)=\dfrac{1}{2}g{{t}^{2}}$
By solving this equation we get the time at which the collision occurs, ‘t’ as
$\Rightarrow {{t}^{2}}=\dfrac{2\left( h-x \right)}{g}$
$\Rightarrow t=\sqrt{\dfrac{2\left( h-x \right)}{g}}$
Now we can apply the second equation of motion on the ball B. thus we get,
${{s}_{B}}={{u}_{B}}t+\dfrac{1}{2}\left( -g \right){{t}^{2}}$, here we take the acceleration as $\left( -g \right)$ because the acceleration of the ball is in the upward direction.
We know that the displacement of the ball B is ‘x’. Hence,
\[\Rightarrow x={{u}_{B}}t-\dfrac{1}{2}g{{t}^{2}}\]
We can also substitute the expression for time from the previous equation. Thus we get,
\[\Rightarrow x={{u}_{B}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)-\dfrac{1}{2}g\left( \dfrac{2\left( h-x \right)}{g} \right)\]
By solving this equation we get
\[\Rightarrow x={{u}_{B}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)-\left( h-x \right)\]
\[\Rightarrow x={{u}_{B}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)+x-h\]
\[\Rightarrow 0={{u}_{B}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)-h\]
From this we he the total height ‘h’ as,
\[\Rightarrow h={{u}_{B}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)\]
Now we have the third equation of motion as
${{v}^{2}}-{{u}^{2}}=2as$, were ‘v’ is the final velocity, ‘’u’ is the initial velocity, ‘a’ is the acceleration and ‘s’ is the displacement.
For the ball A we can write this equation as,
${{v}_{A}}^{2}-{{u}_{A}}^{2}=2g\left( h-x \right)$
Since ${{v}_{A}}=2{{v}_{B}}$ and ${{u}_{A}}=0$, we can write this as,
$\Rightarrow {{\left( 2{{v}_{B}} \right)}^{2}}=2g\left( h-x \right)$
From this we get the final velocity of the ball B as,
$\Rightarrow 4{{v}_{B}}^{2}=2g\left( h-x \right)$
$\Rightarrow {{v}_{B}}^{2}=\dfrac{2g\left( h-x \right)}{4}$
$\Rightarrow {{v}_{B}}=\sqrt{\dfrac{g\left( h-x \right)}{2}}$
Now by applying the third equation of motion on the ball B, we get
${{v}_{B}}^{2}-{{u}_{B}}^{2}=2\left( -g \right)x$
By applying the value for final velocity of the ball B in the above equation, we get
$\Rightarrow \left( \dfrac{g\left( h-x \right)}{2} \right)-{{u}_{B}}^{2}=-2gx$
By solving this we get the initial velocity of the ball B as,
$\Rightarrow {{u}_{B}}^{2}=\left( \dfrac{g\left( h-x \right)}{2} \right)+2gx$
$\Rightarrow {{u}_{B}}^{2}=\dfrac{gh-gx}{2}+2gx$
$\Rightarrow {{u}_{B}}^{2}=\dfrac{gh+3gx}{2}$
$\Rightarrow {{u}_{B}}=\sqrt{\dfrac{gh+3gx}{2}}$
We have the equation for height of the building as,
 \[\Rightarrow h={{u}_{B}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)\]
By applying for ‘${{u}_{B}}$’ in this equation, we get the total height as
\[\Rightarrow h=\sqrt{\dfrac{gh+3gx}{2}}\left( \sqrt{\dfrac{2\left( h-x \right)}{g}} \right)\]
\[\Rightarrow h=\sqrt{\dfrac{gh+3gx}{2}\times \dfrac{2\left( h-x \right)}{g}}\]
\[\Rightarrow h=\sqrt{\left( h+3x \right)\left( h-x \right)}\]
\[\Rightarrow h=\sqrt{{{h}^{2}}+3hx-xh-3{{x}^{2}}}\]
\[\Rightarrow {{h}^{2}}={{h}^{2}}+2hx-3{{x}^{2}}\]
\[\Rightarrow 2hx-3{{x}^{2}}=0\]
$\Rightarrow x\left( 2h-3x \right)=0$
From this we can say that either,
$x=0$ or $\left( 2h-3x \right)=0$
$\Rightarrow 3x=2h$
$\Rightarrow x=\dfrac{2}{3}h$
Thus the distance where the collision occurs is $\dfrac{2}{3}$ times of the total height.
Therefore we get the fraction of the height of the building where the collision occurs as $\dfrac{2}{3}$.

So, the correct answer is “Option B”.

Note: Here at the end, we get the quadratic equation
\[2hx-3{{x}^{2}}=0\]
We know that for a quadratic equation,
${{a}^{2}}x+bx+c=0$
To find the value of ‘x’, we can have the expression,
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
In the case of \[2hx-3{{x}^{2}}=0\], we have
$a=-3,b=2h,c=0$
Therefore we can write,
$\Rightarrow x=\dfrac{-\left( 2h \right)\pm \sqrt{{{\left( 2h \right)}^{2}}-\left( 4\times -3\times 0 \right)}}{2\times \left( -3 \right)}$
$\Rightarrow x=\dfrac{-2h\pm \sqrt{4{{h}^{2}}}}{-6}$
$\Rightarrow x=\dfrac{-2h\pm 2h}{-6}$
By solving this we get two values of x,
$\Rightarrow x=\dfrac{-2h+2h}{-6},\dfrac{-2h-2h}{-6}$
$\Rightarrow x=\dfrac{0}{-6},\dfrac{-4h}{-6}$
$\Rightarrow x=0,\dfrac{2h}{3}$
In this method also we get the same solution (We neglect $x=0$ because height where the collision occurs cannot be zero).