Question

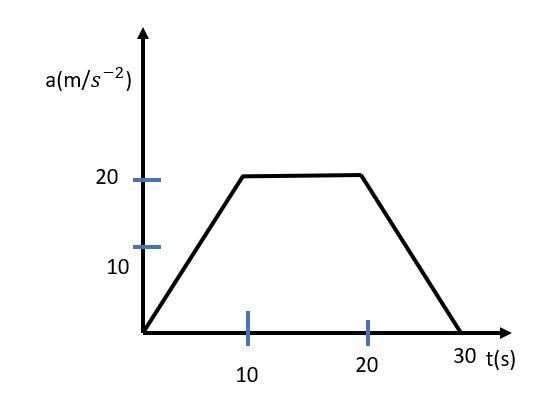
What is the average acceleration in the first $20$ seconds?

Answer 1

Hint: Note that in v-t graph a horizontal line (zero slope) means that the object has zero acceleration and moves at uniform velocity. If a line has a positive slope on a graph, we state that the object has positive acceleration; if the line has a negative slope, we suppose that it has negative acceleration.

Complete answer:

$\textit{average acceleration} = \dfrac{\textit{change in velocity}}{\textit{change in time}}$
 $a = \dfrac{\Delta v}{\Delta t}$
$ \Delta v = \int a dt = \textit{area under a-t curve}$
We have to find the average acceleration for the first 20 seconds.
$a = \dfrac{\textit{area(first triangle+rectangle)} }{20-0}$
$a = \dfrac{\dfrac{1}{2} \times 10 \times 20 + 20\times 10}{20-0}= \dfrac{100+200}{20} = \dfrac{300}{20}$
$a=15 m s^{-1}$
Average acceleration for first 20 seconds, $a=15 m s^{-1}$

Additional Information:
Acceleration is a vector term that consists of both magnitudes and direction. It is the second derivative of distance to time, or it is the first derivative of velocity to time. If an object slows down, then its acceleration will be in the reverse direction of its motion or oppose the motion.

Note:
Acceleration determines how an object changes its speed with respect to time. A body is accelerating means it is changing its speed with respect to time. If a body changes its speed with the same amount in the same interval of time then the body possesses constant acceleration. If the body is not changing its speed then the body is not accelerating.