Question

At what time would the car be farthest from its original starting position?

$\begin{align}
  & \text{A}\text{. }2\text{ seconds} \\
 & \text{B}\text{. 4 seconds} \\
 & \text{C}\text{. 6 seconds} \\
 & \text{D}\text{. 8 seconds} \\
\end{align}$

Answer 1

- Hint: Acceleration versus time graph gives the value of acceleration of body at a particular moment and the trend in variation of velocity of the body over a period of time. The area under the acceleration-time graph in a time frame gives the change in velocity of the body in that particular time interval.

Complete step-by-step solution
Acceleration versus time graphs tells us about the velocity of a body the same way velocity versus time graphs tell us about the displacement of the body. The change in velocity in a given time frame, or interval, is equal to the area under the acceleration-time graph during the same time interval.
Explanation of an Acceleration-Time Graph:
The vertical axis in the acceleration-time graph represents the acceleration of the body. The reading of the value of the graph at a particular time will fetch us the acceleration of the body in meters per second squared for that particular moment of time.
The slope of the acceleration-time graph represents a quantity known as jerk. Jerk is defined as the rate of change of acceleration of a body.
The area under the acceleration-time graph represents the change in velocity. Or, we can say that the area under the acceleration-time graph for a certain interval of time is equal to the change in velocity of the body during that time interval.
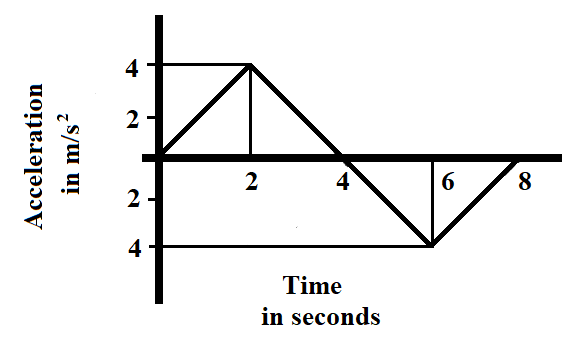
We are given an acceleration-time graph of a car,
The area under the curve represents the change in velocity. The car begins from the position of rest with an increasing positive velocity. After 4 seconds, the car begins to slow and the area under the curve from 4 to 8 seconds counters the increase in velocity from 0 to 4 seconds, bringing the car to rest.
The car does not change its direction during the whole motion and was moving away from the original starting point.
Therefore,
$t=8\text{ seconds}$
The car would be the farthest from the original starting position at 8 seconds.
Hence, the correct option is D.

Note: In an acceleration-time graph, the slope of the graph represents a quantity known as jerk. Jerk is described as the rate of change of velocity of a body, while the under the curve of acceleration-time graph gives the change in velocity of the body. It should be noted that the area does not give the velocity of the body at a particular moment but the change in velocity over a time interval.