Question

At what time, between nine o’clock and ten o’clock, are the hands of a clock in the opposite direction?
A. \[9\] hours \[17\dfrac{8}{{11}}\] minutes
B. \[9\] hours \[21\dfrac{9}{{11}}\] minutes
C. \[9\] hours \[23\dfrac{9}{{11}}\] minutes
D. \[9\] hours \[48\dfrac{9}{{11}}\] minutes
E. \[9\] hours \[16\dfrac{4}{{11}}\] minutes

Answer 1

Hint: We need to find the time at which the hands of a clock ( minute hand and hour hand ) are in the opposite direction not the whole day but between nine o’clock and ten o’clock . Between nine o’clock and ten o’clock ‘hour hand’ lies between \[9\] and \[10\]. In one hour ‘minute hand ’ gains \[{330^0}\] or \[55\] minute space .

Complete step by step answer:
We need to find at what time ‘minute hand’ will be at the opposite of ‘hour hand’ .
The large hand on a clock that points to the minute is called ‘minute hand’. The small hand denotes hour, which is why they are called ‘hour hand ’. At \[9\] o’clock ‘minute hand’ is at 12 and ‘hour hand ’ is at 9 . So at \[9\] o'clock the minute hand is behind the ‘hour hand ’ by \[9 \times 5\]= \[45\] minute space .

Minute hand will be the opposite of the hour hand if it is between \[3\] and \[4\] . As \[3\] and \[4\] is opposite of \[9\] and \[10\]. As ‘minute hand ’ between \[3\] and \[4\] means \[15\] to \[20\] minutes we can assume that ‘hour hand ’ will be near to \[9\].So ‘ minute hand’ has to gain \[3 \times 5\] = \[15\] minute space as \[3\] is opposite to \[9\]. In one hour ‘minute hand’ moves \[{360^0}\]

In one hour ‘hour hand ’ moves \[\dfrac{{{{360}^0}}}{{12}}\] = \[{30^0}\]. So In one hour ‘minute hand ’ gains \[{360^0} - {30^0} = {330^0}\] which means \[55\] minutes space . Gain of \[55\] minutes space achieved in \[60\] minutes .So gain of \[15\] minutes space achieved in \[\dfrac{{60}}{{55}} \times 15\] minutes = \[\dfrac{{180}}{{11}}\] minutes = \[16\dfrac{4}{{11}}\] minutes .

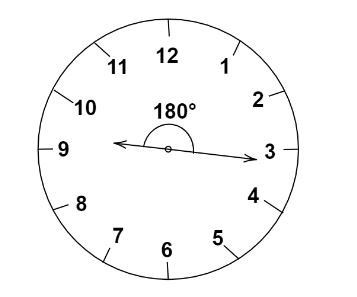
So at \[9\] hours \[16\dfrac{4}{{11}}\] minutes both the two hands of the watch will be in opposite directions between nine o’clock and ten o’clock .

Therefore, option (E) is the correct answer.

Note: Careful about minute and minute space . minute space denotes the space or angle minute hand moves but minute represents time . Be attentive about calculation how much minute space ‘minute hand’ has to gain . Be extra careful about the portion where we deduce gain of \[55\] minutes space achieved in \[60\] minutes.