Question

At what time between, four o’clock & five o’clock, are the hands \[2\]minutes space apart?

Answer 1

Hint: Clock concept: - The dial of the clock is circular in shape and was divided into \[60\]equal minute space.
\[60\]minute space traces an angle \[{360^0}\]
\[1\]minute space traces an angle \[{60^0}\].


Complete step by step solution:
Minute spaces: The face or dial of watch is a circle whose circumference is divided into \[60\]equal parts, called minute spaces.
Hour hand & Minute hand: A clock has two hands, the smaller one is called the hour hand or shorthand, while the larger one is called minute hand or long hand.
In \[60\]equal minutes, the minute hand gains \[55\]minutes on the hour on the hour hand.
When the two hands are at right angles, they are \[15\]minutes spaces apart.
Angle traced by hour hand in \[12\]hours \[ = {360^0}\].
Angle traced by minute hand in \[60\]min \[ = {360^0}\].
Therefore,

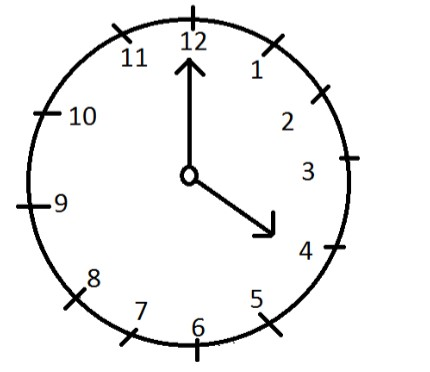
At 4 o’clock the two hands are 20-minute spaces apart.

To be in 2 minute, they must be 2 minute spaces apart.
Minute hand will have to gain \[\left( {20 + 2 = 22} \right)\]minute spaces.
As we know that,
\[55\]minute spaces are gained in \[60\]minute.
\[22\]minute spaces are gained in \[\dfrac{{60}}{{55}} \times 2\]minute\[ = 24\]minute.
Hence the hands will be \[2\]minute apart at \[24\]minute past.

Note: If the clock or watch indicates \[6\]hour \[10\]minute when the correct time is \[6\], it is said that the clock is \[10\]minute too fast.
If it indicates \[6:40\]when the correct time is \[7\], it is said to be \[20\]min slow.