Question

At what angle should the two force vectors $2F$ and $\sqrt 2 F$ act so that the resultant vector is $\sqrt {10} F$ ?

Answer 1

Hint: The resultant is the vector sum of two or more vectors. This can be found out using vector addition methods like the triangle law, parallelogram law and the polygon law.
When two forces act making an angle $\theta $ with each other, then their resultant is given as $R = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } $ .

Complete step by step solution:
The diagrammatic representation is as follows

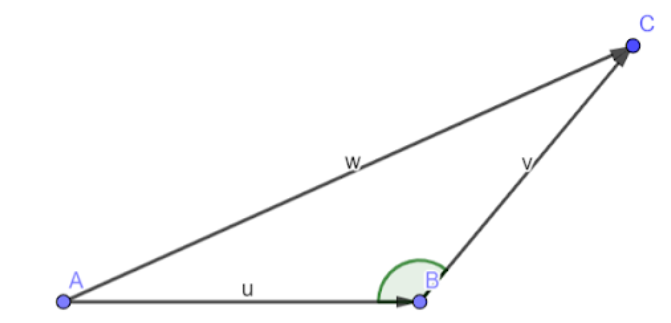
Here u and v are given vectors and w is the resultant vector. The formula can be derived following the triangle law of vector addition.
In this question, we are given the magnitude of two vectors. We shall also assume the angle between them to be $\theta $ . Given the value of the resultant of the two vectors, we can plug in these into the formula of the resultant of the two vectors to get the value of $\theta $ since it will be the only variable in the equation.
 Complete step by step answer: Given two vectors $2F$ and $\sqrt 2 F$. Their resultant is given as $\sqrt {10} F$
Let the angle made by the two vectors be $\theta $.
Substituting the values in the formula $R = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } $ we get,
$\sqrt {10} F = \sqrt {{{(2F)}^2} + {{(\sqrt 2 F)}^2} + 2 \times \sqrt 2 F \times 2F\cos \theta } $
Here $R = \sqrt {10} F\,,\,{F_1} = 2F\,,\,{F_2} = \sqrt 2 F$
Further solving the equation,
$\sqrt {10} F = \sqrt {4{F^2} + 2{F^2} + 4\sqrt 2 {F^2}\cos \theta } $
$ \Rightarrow \sqrt {10} F = \sqrt {6{F^2} + 4\sqrt 2 {F^2}\cos \theta } $
Squaring both sides,
$10{F^2} = 6{F^2} + 4\sqrt 2 {F^2}\cos \theta $
Now solving,
$4{F^2} = 4\sqrt 2 {F^2}\cos \theta $
$ \Rightarrow 1 = \sqrt 2 \cos \theta $
$ \Rightarrow \cos \theta = \dfrac{1}{{\sqrt 2 }}$
$\theta = {\cos ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$
So, the final answer is $\theta = {\cos ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$.

Note:
The arrowheads on the vectors signify their direction. It is imperative to note the direction of vectors while calculating the resultant. The direction could be different as given in the triangle law and so the angle between the vectors would change accordingly. If the direction of one of the vectors is opposite then the angle between the vectors becomes $\pi - \theta $ .