Question

At what angle should a projectile with initial velocity $'v'$ be thrown, so that it achieves its maximum range?

Answer 1

Hint:Let us get some ideas about projectiles. Any object thrown by the application of force is referred to as a projectile.An object launched into space and permitted to move freely under the influence of gravity and air resistance is also referred to as a spacecraft. Although projectiles can be any object in motion across space (for example, a thrown baseball, kicked football, fired bullet, thrown arrow, or stone released from a catapult), they are most typically used in warfare and sports. Projectile trajectories are analysed using mathematical equations of motion.

Complete step-by-step solution:

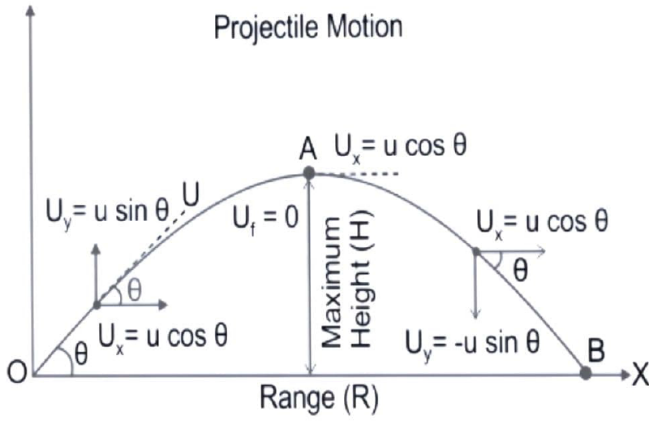
Total time of flight $ = \dfrac{{2\,u\,\sin \theta }}{g}$
Range of projectile $ = \dfrac{{{u^2}\,\sin 2\theta }}{g}$
Maximum Height $ = \dfrac{{{u^2}\,{{\sin }^2}\theta }}{{2g}}$
Where, u = projected speed
$\theta = $angle at which an object is thrown from the ground.
$g = $acceleration due to gravity $ = \,9.8\,m/{s^2}$
Maximum Range: During projectile motion, it is the object's largest distance travelled.
The maximum horizontal range is attained when the projection angle is \[{45^ \circ }\] degrees.
Angle for maximum Vertical range $ = {90^ \circ }$
For maximizing the vertical range, $\sin \theta $must be maximum
which is $\sin \theta = 1$
$\theta = {90^ \circ }$

Note:The propelling force is the most important force applied to the ‘projectile' in projectile motion; in this case, the propelling forces are the muscles that act upon the ball to make it move; the stronger the force applied, the more propelling force, which means the projectile (the ball) will travel farther; and the stronger the force applied, the more the projectile (the ball) will move further due to the pushing force.