Question

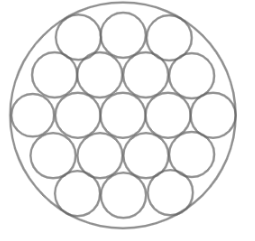
At the beginning of a carrom game the coins are arranged in the central circle of the board as shown. What is the area in (square inches) of the central circle not occupied by the coins if the radius of each coin is $ \dfrac{1}{2}$ an inch?

Answer 1

Hint: Start by drawing a rough diagram of the situation given in order to have a better understanding of the situation. Find the area of one coin using the formula $ \pi {{\left( radius \right)}^{2}}$ and multiply it by 19 to get the total area occupied by the coins. Now if you see the line passing through the centre of the 5 central circles lying in a row, it is the diameter of the larger circle. So, the diameter of the larger circle is 5 times the diameter of the coins, i.e., radius will also be 5 times. So, as you know the radius, find its area and subtract the area occupied from it to get the unoccupied area.

Complete step-by-step answer:
To start with the question let us draw the diagram of the park with the road along its boundary for better visualisation.

Let us first find the total area occupied by the coins. For doing so, we will find the area of 1 coin and multiply it by 19, as there are a total of 19 coins. It is given that the radius of a coin is half inches and we know that the area of a circle is $ \pi {{\left( radius \right)}^{2}}$ .
$ \text{Area of one coin}=\pi {{\left( \dfrac{1}{2} \right)}^{2}}=\dfrac{\pi }{4}inc{{h}^{2}}$
$ \text{Area occupied by coins}=19\times \dfrac{\pi }{4}=\dfrac{19\pi }{4}inc{{h}^{2}}$
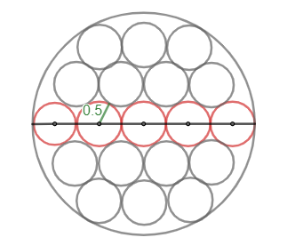
Now if you see the line passing through the centre of the 5 central circles lying in a row, it is the diameter of the larger circle. So, the diameter of the larger circle is 5 times the diameter of the coins, i.e., radius will also be 5 times which is equal to $ \dfrac{5}{2}$ . So, as you know the radius, find its area and subtract the area occupied from it to get the unoccupied area.
$ \therefore \text{The area of the large circle}=\pi \times {{\left( \dfrac{5}{2} \right)}^{2}}=\dfrac{25\pi }{4}inc{{h}^{2}}$
So, the unoccupied area is:
$ \text{Area of larger circle}-\text{occupied area}=\dfrac{25\pi }{4}-\dfrac{19\pi }{4}=\dfrac{6\pi }{4}=\dfrac{3\pi }{2}inc{{h}^{2}}$
Therefore, the unoccupied area is $ \dfrac{3\pi }{2}inc{{h}^{2}}$ .

Note: The key to this question is to draw the correct diagram of the situation given in the question and identifying the diameter of the larger circle. You should remember the formula of area and perimeter of the circle. Also, be careful about the calculation part as there is a high chance of making a mistake in the calculation part.