Question

At the base of a mountain the elevation of its summit is$45^\circ $. After ascending 600 meters towards the mountain upon incline of$30^\circ $, the elevation changes to$60^\circ $. Find the height of the mountain?
A. 300 m
B. $300\sqrt 3 $ m
C. $200\sqrt 3 \left( {1 + \sqrt 3 } \right)$ m
D. $300\left( {\sqrt 3 - 1} \right)$ m

Answer 1

Hint: First try to express the problem with the help of figure and then apply the trigonometric ratios to find the value of $x$ and$y$ that helps in the calculation of the height of the mountain.

According to the question, the diagram expressing the given problem is given below:

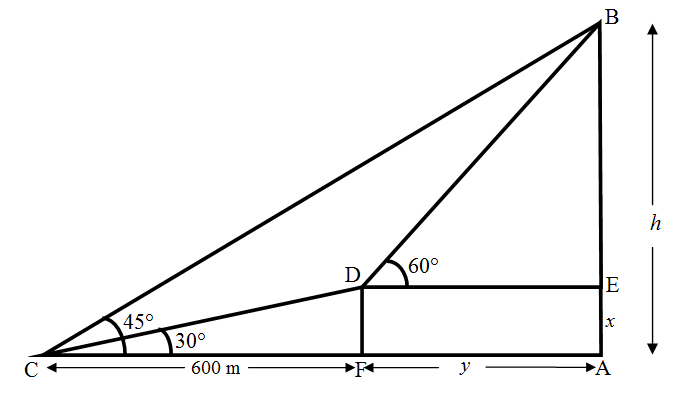
It is assumed in the figure that $AE = DF = x$ and$AF = DE = y$.
Assume that the height of the mountain is $h$ ,then
$AB = h$
Apply the trigonometric ratio in the triangle $\Delta CDF$,
$\tan \theta = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent}}}}$
Substitute $30^\circ $ as the value of$\theta $ and the length $DF = EA = x$ in the above trigonometric formula,
$\tan 30^\circ = \dfrac{{DF}}{{CF}}$
Substitute$\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ and 600 as the value of $CF$ in the above trigonometric expression,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{DF}}{{600}}$
Solve the above equation for the value of $DF$,
$DF = \dfrac{{600}}{{\sqrt 3 }}$
$DF = \dfrac{{600}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}$
$DF = \dfrac{{600\sqrt 3 }}{3}$
$DF = 200\sqrt 3 $
Therefore, the value of $x$ is $200\sqrt 3 $.
Similarly in$\Delta ACB$ ,
Using the trigonometric ratio,
$\tan \theta = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$
Substitute $45^\circ $ as the value of$\theta $in the above trigonometric formula,
$\tan 45^\circ = \dfrac{{AB}}{{CA}}$
Substitute$\tan 45^\circ = 1$,
 $1 = \dfrac{{AB}}{{CA}}$
$CA = AB$
In the above figure,
$CA = CF + FA$
$CA = 600 + y$
Substitute $h$ as the value of $AB$and $600 + y$ as the value of$CA$,
$
  h = 600 + y \\
  y = h - 600 \\
$
In$\Delta BDE$,
$\tan 60^\circ = \dfrac{{BE}}{{ED}}$
Substitute $\sqrt 3 $as the value of$\tan 60^\circ $,$h - x$as the value of $BE$and $y$ as the value of ED.
$\sqrt 3 = \dfrac{{h - x}}{y}$
Substitute the values$x = 200\sqrt 3 $ and$y = h - 600$:
$\sqrt 3 = \dfrac{{h - 200\sqrt 3 }}{{h - 600}}$
Solve the equation for the value of $h$:
$\sqrt 3 = \dfrac{{h - 200\sqrt 3 }}{{h - 600}}$
$\sqrt 3 h - 600\sqrt 3 = h - 200\sqrt 3 $
$\sqrt 3 h - h = 600\sqrt 3 - 200\sqrt 3 $
$h\left( {\sqrt 3 - 1} \right) = 400\sqrt 3 $
$h = \dfrac{{400\sqrt 3 }}{{\sqrt 3 - 1}}$
Now, multiply and divide the equation by the conjugate of the denominator:
$h = \dfrac{{400\sqrt 3 }}{{\sqrt 3 - 1}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}$
$h = \dfrac{{400\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$
$h = \dfrac{{400\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}$
$h = 200\sqrt 3 \left( {\sqrt 3 + 1} \right)$
So, the height of the mountain is $200\sqrt 3 \left( {\sqrt 3 + 1} \right)$m.
Therefore, the option (C) is correct.

[Note:Try to find the values of $x$ and$y$ in the terms of $h$, it makes easy to calculate the height of the mountain.]