Question

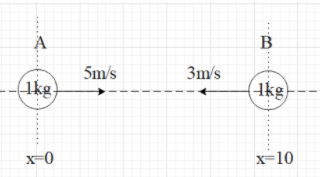
At t=0, the position and velocities of two particles are as shown in figure. They are kept on a smooth surface and are mutually attracted by gravitational force. Find the position of centre of mass at t = 2s.

A. x = 5m
B. x = 7m
C. x = 3m
D. x = 2m

Answer 1

Hint: Check whether the net force on the system is zero. Then find the velocity of the centre of mass of the two particles at time t=0. Also find the position of the centre of mass at t=0. Then calculate the distance moved by the centre of mass in 2s. With this find the position of the centre of mass at t=2s.
Formula used:
${{v}_{com}}=\dfrac{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
${{x}_{com}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
$x=vt$

Complete answer:
The two particles are said to be mutually attracted by gravitational force. This means that particle A will attract particle B towards itself and particle B will attract particle A towards itself. As a result, the two will move towards each other.
The magnitude of the force that A exerts on B is equal to the magnitude of the force that B exerts on A. Therefore, there are two forces acting on the system of the two particles. However, the forces are opposite in direction and equal in magnitude. Hence, the net force on the given system is zero.
When the net force on a system of particles is zero, the velocity of the centre of mass of the system remains constant. Therefore, let us find the velocity of the centre of mass at time t=0.
The velocity of the centre of mass of a system of two particles (when the particles are moving in one dimension) is given as ${{v}_{com}}=\dfrac{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$ ….. (i).
Here, ${{m}_{1}}={{m}_{2}}=1kg$
${{v}_{1}}=5m{{s}^{-1}}$ and ${{v}_{3}}=-3m{{s}^{-1}}$ (because B is moving in the direction of negative x-axis).
Substitute the values in (i).
$\Rightarrow {{v}_{com}}=\dfrac{1(5)+1(-3)}{1+1}=\dfrac{2}{2}=1m{{s}^{-1}}$.
This means that constant velocity of the centre of mass is $1m{{s}^{-1}}$.
Therefore, in 2 seconds the centre of mass will be displaced to the right by $x=vt=1\times 2=2m$.
Let us now calculate the position of the centre of mass at t=0 by using the formula ${{x}_{com}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$ .
From the figure we get to know that ${{x}_{1}}=0$ and ${{x}_{2}}=10m$
${{x}_{com}}=\dfrac{1(0)+1(10)}{1+1}=\dfrac{10}{2}=5m$.
Therefore, the position of the centre of mass at t=2s is $5+2=7m$.

Hence, the correct option is B.

Note:
Note that in a system of two particles, the centre of mass of the two particles is always on the line joining the two particles. If the masses of the particles are equal then the centre of mass is located at the midpoint of the line segment joining the two.
Also note that only the centre of mass is moving with a constant velocity. Whereas the two particles are accelerating under force of gravity.