
At 5 : 20, the angle formed between the two hands of a clock is
A. Obtuse
B. Right
C. Acute
D. None of these
Answer
596.7k+ views
Hint: We will first try to find the least angle that should be there, by using the fact that each hour contains $ 30{}^\circ $ , so (5 - 4) = 1 contains $ 1\times 30=30{}^\circ $ . Then we will apply the fact that the hour hand advances one full number for each complete rotation of the minute hand through $ 360{}^\circ $ , which means that the minute hand advances 20 minutes or $ \dfrac{1}{3} $ of an hour.
Complete step-by-step answer:
In the question we have been asked to find the angle between the minute hand and the hour hand of the clock if the clock shows 5 : 20 A.M. We know that the angle in a clock is $ 360{}^\circ $ . In a clock the numbers are labelled from 1 to 12 in the perimeter of a circle, thus dividing the clock into 12 sections. So, we can say that if the sections are equally divided, then the angle subtended by each section will be $ \dfrac{360{}^\circ }{12}=30{}^\circ $ . We also know that in the numbers represented on a clock, every successive section has a difference of 5 minutes between them. So, we can say that for a 5 minutes interval, it contains $ 30{}^\circ $ . So, in one minute, it contains $ \dfrac{360{}^\circ }{5}=6{}^\circ $ .
In the question, we are given the reading on the clock as 5 : 20, which means that the minute hand is at 4 and the hour hand is slightly past 5, assuming that the hands of the clock rotate relatively smoothly. So, if (5 - 4) is 1, then it will be $ 1\times 30=30{}^\circ $ ( $ 30{}^\circ $ for each hour interval) or $ 30{}^\circ $ will be the least angle between the hands, but the answer is incomplete. Now, we know that the hour hand advances one full number for each hour. So, each hour is represented by a complete rotation of the minute hand through $ 360{}^\circ $ . This means that when the minute hand advance 20 minutes or $ \dfrac{1}{3} $ of an hour, the hour hand also advances by one-third of those $ 30{}^\circ $ or $ \dfrac{1}{3}\times 30{}^\circ =10{}^\circ $ . So, the angle between the hands is $ 30{}^\circ +10{}^\circ =40{}^\circ $ . Hence, the angle between the minutes and hour hand of the clock with a reading of 5 : 20 is $ 40{}^\circ $ . And since the angle is less than $ 90{}^\circ $ , it is an acute angle.
Therefore, the correct answer is option C.
Note: There is a formula to solve these kinds of problems in a shortcut method. It is given as $ \left| \dfrac{11M}{2}-30H \right| $ , where M means the reading of the minute hand and H means the reading of the hour hand. Since we were not asked the magnitude of the angle, we could have drawn the figure of the clock showing 5 : 20 and then reached a conclusion.
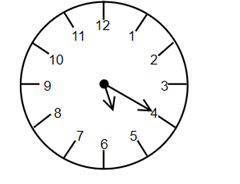
Complete step-by-step answer:
In the question we have been asked to find the angle between the minute hand and the hour hand of the clock if the clock shows 5 : 20 A.M. We know that the angle in a clock is $ 360{}^\circ $ . In a clock the numbers are labelled from 1 to 12 in the perimeter of a circle, thus dividing the clock into 12 sections. So, we can say that if the sections are equally divided, then the angle subtended by each section will be $ \dfrac{360{}^\circ }{12}=30{}^\circ $ . We also know that in the numbers represented on a clock, every successive section has a difference of 5 minutes between them. So, we can say that for a 5 minutes interval, it contains $ 30{}^\circ $ . So, in one minute, it contains $ \dfrac{360{}^\circ }{5}=6{}^\circ $ .
In the question, we are given the reading on the clock as 5 : 20, which means that the minute hand is at 4 and the hour hand is slightly past 5, assuming that the hands of the clock rotate relatively smoothly. So, if (5 - 4) is 1, then it will be $ 1\times 30=30{}^\circ $ ( $ 30{}^\circ $ for each hour interval) or $ 30{}^\circ $ will be the least angle between the hands, but the answer is incomplete. Now, we know that the hour hand advances one full number for each hour. So, each hour is represented by a complete rotation of the minute hand through $ 360{}^\circ $ . This means that when the minute hand advance 20 minutes or $ \dfrac{1}{3} $ of an hour, the hour hand also advances by one-third of those $ 30{}^\circ $ or $ \dfrac{1}{3}\times 30{}^\circ =10{}^\circ $ . So, the angle between the hands is $ 30{}^\circ +10{}^\circ =40{}^\circ $ . Hence, the angle between the minutes and hour hand of the clock with a reading of 5 : 20 is $ 40{}^\circ $ . And since the angle is less than $ 90{}^\circ $ , it is an acute angle.
Therefore, the correct answer is option C.
Note: There is a formula to solve these kinds of problems in a shortcut method. It is given as $ \left| \dfrac{11M}{2}-30H \right| $ , where M means the reading of the minute hand and H means the reading of the hour hand. Since we were not asked the magnitude of the angle, we could have drawn the figure of the clock showing 5 : 20 and then reached a conclusion.

Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




