Question

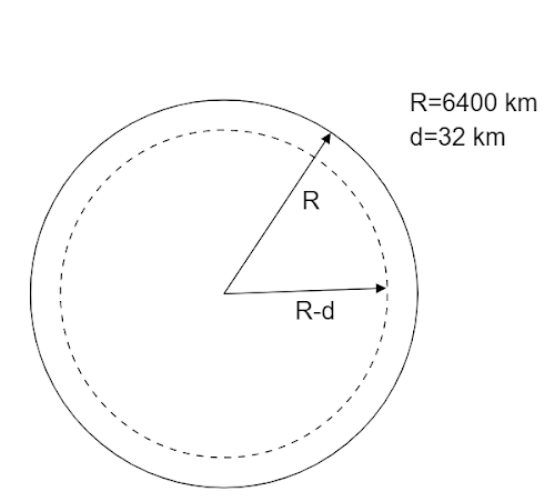
Assuming that the Earth is a sphere of uniform mass density, find the percentage decrease in the weight of a body when taken to the end of a tunnel $32{\text{ }}km$ below the surface of Earth. Radius of Earth = $6400{\text{ }}km$.
(A) $0.6$
(B) $0.5$
(C) $0.7$
(D) $0.8$

Answer 1

Hint: We will use the force of gravitation to find out the solution. We have to change the mass in terms of density as the total mass changes. Then by comparing the equations of force of gravitation, we will find the decreased weight.

Complete step by step answer:
The generalized formula for the force of gravitation is,
$F = \dfrac{{GMm}}{{{r^2}}} - - - - \left( 1 \right)$
The variables are named as,
$F = $ force of gravitation
$G = $ Universal gravitational constant
$M = $ Mass enclosed on Earth.
$m = $ mass of the body
$r = $ displacement between the center of the earth and the body

Now $a = g$ for this case as acceleration due to gravity only works,
Now equation $\left( 1 \right)$ can be written as,
$mg = \dfrac{{GMm}}{{{r^2}}} - - - - \left( 2 \right)$
When the body is on the surface of the Earth then, $M = \rho \times V$ where $M = $ mass, $V = $ Volume and $\rho = $ density.
Let the original weight of the body be $W$.
Thus, the weight of the body will be,
$W = \rho \dfrac{{Gm}}{{{R^2}}} \times \dfrac{4}{3}\pi {R^3} - - - - \left( 3 \right)$
When the body is taken to a depth of $d$ then, the mass under the $R - d$ distance comes as,
$M = \rho \times \dfrac{4}{3}\pi {\left( {R - d} \right)^3}$ and $\rho $ is constant as given in the question that density is uniform
Let the weight of the body $W'$
$W' = \rho \dfrac{{Gm}}{{{{\left( {R - d} \right)}^2}}} \times \dfrac{4}{3}\pi {\left( {R - d} \right)^3} - - - - \left( 4 \right)$
Now comparing equation $\left( 3 \right)$ and $\left( 4 \right)$ we get,
$\dfrac{{W'}}{W} = \dfrac{{\rho \dfrac{{Gm}}{{{{\left( {R - d} \right)}^2}}} \times \dfrac{4}{3}\pi {{\left( {R - d} \right)}^3}}}{{\rho \dfrac{{Gm}}{{{R^2}}} \times \dfrac{4}{3}\pi {R^3}}} = \dfrac{{R - d}}{R}$
Putting the value $R = 6400$ and $d = 32$ we get,
$\dfrac{{W'}}{W} = \dfrac{{6400 - 32}}{{6400}} = 0.995$
$ \Rightarrow W' = 0.995W$
Now, the percentage of decrement of weight is,
$
  \dfrac{{W - W'}}{W} \times 100\% \\
   \Rightarrow \dfrac{{W - 0.995W}}{W} \times 100 = 0.5\% \\
 $
So, the percentage change in decrement of weight when the body is taken to $32{\text{ }}km$ inside the Earth is $0.5\% $.
Hence, the correct option is (B).

Note: There is no change in the mass of a body if it is taken anywhere, only the weight changes. The weight changes because acceleration due to gravity changes at different places. The total mass of the Earth is not considered when it is taken inside the Earth, it operates only in the area enclosed by the body radially. It is just like Gauss’ Law.