Question

Assuming Earth to be spherical, at what approximate height (in Km) above the North Pole, value of g the same as that on the Earth’s surface at the equator?

Answer 1

Hint: Since our Earth is not a uniform non-rotating sphere, acceleration due gravity shows significant variation due to that. Though in the question we have assumed a non-rotating sphere, it still has a rotation. Find the expression for variation in g due to rotation at equator (θ=0) and then equate it to expression for variation in g due to height for a height h at North Pole. Then by substituting all the known values we get the approximate height h.

Formula used:
Expression for variation in g due to Earth’s rotation,
$g'=g-R{{\omega }^{2}}{{\cos }^{2}}\theta $
Expression for variation in g with height,
$g''=\dfrac{g}{{{\left( 1+\dfrac{h}{R} \right)}^{2}}}$

Complete step by step answer:
We know that acceleration due to gravity g varies with depth as well as height. Also, there is a variation in acceleration due to gravity due to Earth’s rotation.

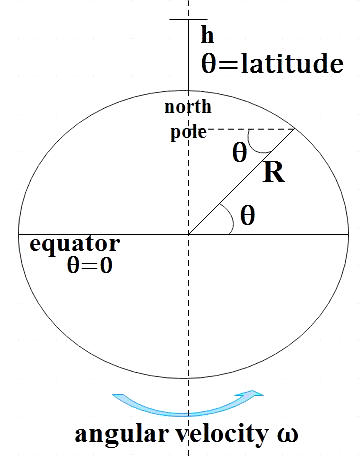
Let us represent the variation in g due to earth’s rotation by$g'$ , then $g'$ is given by the expression,
$g'=g-R{{\omega }^{2}}{{\cos }^{2}}\theta $ ……………………… (1)
Let us represent the variation in g due to the variation in height by$g''$ , then $g''$ is given by the expression,
$g''=\dfrac{g}{{{\left( 1+\dfrac{h}{R} \right)}^{2}}}$ ………………………… (2)
The term ‘g’ in both (1) and (2) has the value of,
$g=9.8m{{s}^{-2}}$
If our Earth had been a perfect sphere of uniform mass density and non-rotating, it would have produced gravitational fields of uniform magnitude at all points on its surface. However, in reality earth is spherically asymmetric as well as rotating. But in the given question we have made an assumption that the Earth is a uniform sphere.
Due to rotation of Earth the variation in acceleration due to gravity at equator becomes,
$g'=g-R{{\omega }^{2}}{{\cos }^{2}}\theta $
But, at equator we have θ=0, so,
$\Rightarrow g'=g-R{{\omega }^{2}}{{\cos }^{2}}\left( 0 \right)$
$\Rightarrow g'=g-R{{\omega }^{2}}$ ………………………….. (3)
For some height above the North Pole, there definitely will be a variation in acceleration due to gravity which is given by,
$g''=\dfrac{g}{{{\left( 1+\dfrac{h}{R} \right)}^{2}}}$ …………………………….. (4)
We are supposed to find the height h at which the value of g is the same as that on the Earth’s surface at the equator.
So, let h be the height above the North Pole for which g has the same value as that on the Earth’s surface at equator. We could now equate (3) and (4), and so we get,
$\Rightarrow g-R{{\omega }^{2}}=\dfrac{g}{{{\left( 1+\dfrac{h}{R} \right)}^{2}}}$
$\Rightarrow R{{\omega }^{2}}=g\left( 1-{{\left( 1+\dfrac{h}{R} \right)}^{-2}} \right)$……………………. (5)
For$h\ll R$ ,
${{\left( 1+\dfrac{h}{R} \right)}^{-2}}=\left( 1-\dfrac{2h}{R} \right)$
Now (5) becomes,
$\Rightarrow R{{\omega }^{2}}=g\left( 1-1+\dfrac{2h}{R} \right)$
$\Rightarrow R{{\omega }^{2}}=\dfrac{2hg}{R}$
$\Rightarrow h=\dfrac{{{R}^{2}}{{\omega }^{2}}}{2g}$ ………………………………… (6)
But we know that ω is given by,
$\omega =\dfrac{2\pi }{T}$
Substituting in (6) we get,
$\Rightarrow h=\dfrac{{{R}^{2}}{{\left( \dfrac{2\pi }{T} \right)}^{2}}}{2g}$
R is the radius of curvature of earth = 6400km
T is the time period of rotation of earth =24Hr = 24×3600 seconds
$\Rightarrow h=\dfrac{{{\left( 6400\times {{10}^{3}} \right)}^{2}}{{\left( \dfrac{2\pi }{24\times 3600} \right)}^{2}}}{2\times 9.8}$
$\Rightarrow h=10.97\times {{10}^{3}}m\approx 11km$
Hence, the approximate height above the North Pole for which the value of g is the same as that on the Earth’s surface at equator is 11km.

Note:
The assumption that we took in between the derivation that $h\ll R$ is proven true at the end of the solution. That is $\left( h=11km \right)\ll \left( R=6400km \right)$. Some values like that of g, R will not be given in the question under the assumption that you already know that. So, try keeping such values always in mind.