Question

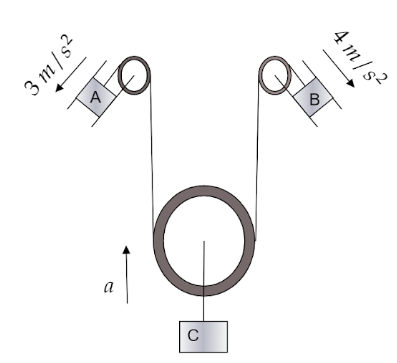
Assuming all the surfaces to be frictionless, acceleration of the block C, shown in the figure is _____ $\dfrac{m}{{{s^2}}}$.

Answer 1

Hint: In this question above we have to find the acceleration of block C and the value of acceleration of block A and B are given. We will consider the distances that block A, B and C may cover due to tension of the string. Then, the double derivative of the equation will give the result.

Complete step by step answer:
Let us consider that the two bodies are suspended by a string. Forces are acting on them.The surfaces given here are also frictionless.Let us now consider that the block A having acceleration of $3{\text{ }}\dfrac{m}{{{s^2}}}$ moves by a distance $x$ as it is acted upon forces or tension of the string.Now, let us assume that block B which is moving with a velocity of ${\text{4 }}\dfrac{m}{{{s^2}}}$ moves by a distance $y$ as it is also acted upon forces or tension of the string.

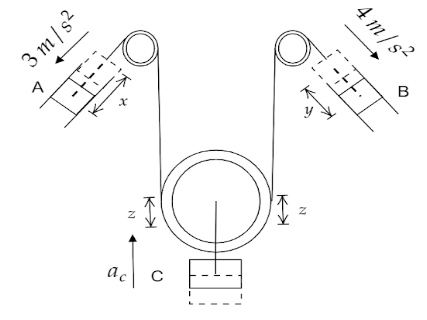
The block is also acted upon tension and its weight and lets it cover a distance of $z$. So, we can easily say that the distance moved by block C is equal to the distance moved by block A and C combined. As the block C is connected with two strings, we have
$z = x$ and $z = y$.
Thus, we now sum these two and get,
$2z = x + y$
$ \Rightarrow z = \dfrac{{x + y}}{2}$
Double derivative of the equation with respect to $t$, we get,
$\dfrac{{{d^2}z}}{{d{t^2}}} = \dfrac{1}{2}\left( {\dfrac{{{d^2}y}}{{d{t^2}}} + \dfrac{{{d^{}}y}}{{d{t^2}}}} \right)$
Double derivative of distance with respect to time gives acceleration,
${a_c} = \dfrac{{{a_a} + {a_b}}}{2}$
Substituting the values of acceleration of block A and C we get,
$\therefore {a_c} = \dfrac{{3 + 4}}{2} = 3.5$

Therefore, the acceleration of block C is $3.5{\text{ }}\dfrac{m}{{{s^2}}}$.

Note:It must be noted that the first derivative of distance with respect to time gives velocity whereas the second derivative of distance with respect to time gives acceleration. As there is no friction there isn’t any opposition in forces, if there was friction between the surfaces, we have to use the tension formula. Also the Block A and B have the same angle of inclination with respect to C.