Question

Assume the bottom of a $16ft$ ladder is pulled out at a rate of $3ft/s$. How do you find the rate at the top of the ladder when it is $10ft$ from the ground?

Answer 1

Hint: To solve this question, we need to use the Pythagoras theorem. On substituting the values of the length and the height of the ladder, we will get the horizontal distance of the bottom end of the ladder from the top point. Then on differentiating the equation obtained after applying the Pythagoras theorem, we will get a relation between the speeds of the top and the bottom points. In that relation, we have to substitute the given height, and the obtained horizontal distance to get the final rate at the top.

Complete step by step solution:
Let us label the ladder as AB whose top end is at the point A and the bottom is at the point B. Let us assume the speed of the point A to be $v$. We represent these in the below figure.

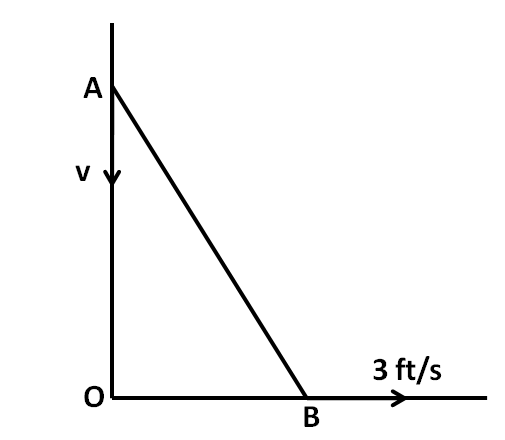
Let us apply Pythagoras theorem in the triangle OAB to get
$\Rightarrow A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}}......\left( i \right)$
According to the question, the length of the ladder is \[AB=16ft\], and the height of the ladder from the ground is given as to be equal to $10ft$, which means that $OA=10ft$. Therefore, we substitute \[AB=16ft\] and $OA=10ft$ in the above equation to get
$\begin{align}
  & \Rightarrow {{16}^{2}}={{10}^{2}}+O{{B}^{2}} \\
 & \Rightarrow 256=100+O{{B}^{2}} \\
\end{align}$
Subtracting $100$ from both the sides, we get
\[\begin{align}
  & \Rightarrow 256-100=100+O{{B}^{2}}-100 \\
 & \Rightarrow 156=O{{B}^{2}} \\
 & \Rightarrow O{{B}^{2}}=156 \\
\end{align}\]
Taking square root both sides, we get
$\begin{align}
  & \Rightarrow OB=\sqrt{156}ft \\
 & \Rightarrow OB=2\sqrt{39}ft \\
\end{align}$
Now, we differentiate the equation (i) with respect to the time ‘t’ to get
$\Rightarrow 2AB\dfrac{d\left( AB \right)}{dt}=2OA\dfrac{d\left( OA \right)}{dt}+2OB\dfrac{d\left( OB \right)}{dt}$
According to the question, we have $\dfrac{d\left( OB \right)}{dt}=3ft/s$, and according to our assumption, $\dfrac{d\left( OA \right)}{dt}=-v$. Also, since the length AB of the ladder is constant, we have $\dfrac{d\left( AB \right)}{dt}=0$. Substituting these in the above equation, we get
\[\begin{align}
  & \Rightarrow 2AB\left( 0 \right)=2OA\left( -v \right)+2OB\left( 3 \right) \\
 & \Rightarrow 0=-2v\left( OA \right)+6OB \\
 & \Rightarrow 2v\left( OA \right)=6OB \\
 & \Rightarrow v=\dfrac{3OB}{OA} \\
\end{align}\]
Finally, substituting $OA=10ft$ and $OB=2\sqrt{39}ft$ as obtained above, we get
\[\begin{align}
  & \Rightarrow v=\dfrac{3\sqrt{39}}{10}ft/s \\
 & \Rightarrow v=0.3\sqrt{39}ft/s \\
\end{align}\]
Hence, the rate at the top of the ladder is equal to \[0.3\sqrt{39}ft/s\].

Note:
Be careful regarding the rates of the quantities while substituting them into the constraint relation. Since the end A is going down, the length OA will decrease and hence the rate $\dfrac{d\left( OA \right)}{dt}$ is taken as negative of v. For solving these types of questions, we must always prefer to draw a figure in accordance with the given information.