Question

Assume that the earth moves around sun in a circular orbit of radius R and there
exists a planet which also moves around the sun in circular orbit with an angular speed twice
as large as that of the earth. The radius of the planet is
$ {\text{A}}{\text{. }}{{\text{2}}^{\dfrac{{ - 2}}{3}}}R \\
{\text{B}}{\text{. }}{{\text{2}}^{\dfrac{2}{3}}}R \\
{\text{C}}{\text{. }}{{\text{2}}^{\dfrac{{ - 1}}{3}}}R \\
{\text{D}}{\text{. }}\dfrac{R}{{\sqrt 2 }} \\ $

Answer 1

Hint: We can make use of Kepler’s third law of periods for the planetary motion. We are given the value of the angular speeds from which we can obtain the time periods of the planets around the sun. Comparing the equations of the third law for two planets, we can get the required answer.
Formula used:
Kepler’s third law of planetary motion, the law of periods, is given as
${T^2} \propto {a^3}$

Complete step-by-step solution:
We know that Kepler’s third law of planetary motion is given as
${T^2} \propto {a^3}$

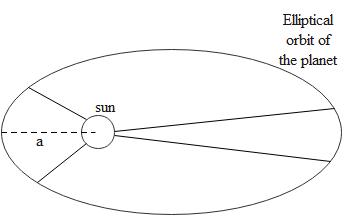
Here T is the time period of a planet around the sun while a represents the length of the semi-major axis of the elliptical path of that planet around the sun. We know that time period is inversely related to angular velocity while if we assume the orbits to be circular then the length of the semi-major axis is directly related to the radius of the circular path of the planet It can be written in terms of the angular velocity in the following way.
$T \propto \dfrac{1}{\omega } \\
  a \propto R \\
\therefore \dfrac{1}{{{\omega ^2}}} \propto {R^3}{\text{ }}...............{\text{(i)}} \\ $
We are given that the radius of the circular orbit of the earth is ${R_1}$ and let ${\omega _1}$ be the angular velocity of the earth around the sun. For another planet, let ${\omega _2}$ be its angular velocity which is given to be twice that of earth. Therefore, we can write
${\omega _2} = 2{\omega _1}$
Let ${R_2}$ be the radius of the circular path of the other planet. Using the equation (i), we can write
$ \dfrac{{R_1^3}}{{R_2^3}} = \dfrac{{\omega _2^2}}{{\omega _1^2}} \\
   \Rightarrow R_2^3 = \dfrac{{\omega _1^2}}{{\omega _2^2}}R_1^3 \\ $
Inserting the known values, we get
$R_2^3 = \dfrac{{\omega _1^2}}{{{{\left( {2{\omega _1}} \right)}^2}}}R_1^3 = \dfrac{{R_1^3}}{4} \\
   \Rightarrow {R_2} = \dfrac{{{R_1}}}{{{2^{\dfrac{2}{3}}}}} \\
   \Rightarrow {R_2} = {2^{\dfrac{{ - 2}}{3}}}{R_1} \\ $
This is the required answer. Hence, the correct answer is option A.

Note: It should be noted from the law of periods that the greater the time period of the planet, the farther away it is from the sun. In terms of the angular velocity, we can say that the nearer planets have greater angular velocity while farther planets have smaller angular velocity.