Question

Assume that the distance of the earth from the moon to be 38,400 km and the angle subtended by the moon at the eye of the person on the earth to be ${31^{'}}$ ,find the diameter of the moon?
a.The diameter of the moon is $3464\dfrac{8}{{63}}km$
b. The diameter of the moon is $3564\dfrac{8}{{63}}km$
c.The diameter of the moon is $346\dfrac{8}{{63}}km$
d.The diameter of the moon is $3664\dfrac{8}{{63}}km$

Answer 1

Hint: Let AB be the diameter of the moon and O be the observer and the diameter of the moon is nothing but the length of the arc of the circle with the centre as the observer and radius as the distance between the moon and earth . We use the formula $\theta = \dfrac{l}{r}$

Complete step-by-step answer:
Let AB be the diameter of the moon and O be the observer

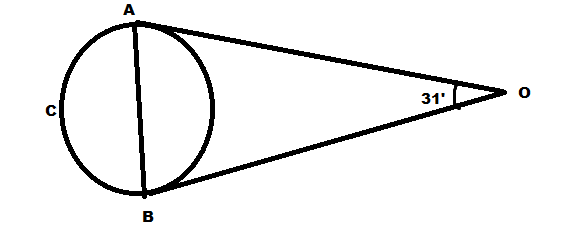
We are given that $\angle AOB = {31^{'}}$
We can convert this into degree by dividing it by 60 and multiplying it by $\dfrac{\pi }{{180}}$
From this we get $\theta = \dfrac{{31}}{{60}}*\dfrac{\pi }{{180}}$ ………(1)
Since the angle subtended by the moon is very small
Its diameter will be equal to the small arc of the circle whose centre is the eye of the observer and radius is the distance of the earth from the moon
And the moon also subtends an angle of 31’ at the centre of this circle
Therefore it is given by the formula
$ \Rightarrow \theta = \dfrac{l}{r}$
Here l = diameter of the moon and r = distance of the earth from the moon
$
   \Rightarrow \dfrac{{31}}{{60}}*\dfrac{\pi }{{180}} = \dfrac{{AB}}{{384400}} \\
   \Rightarrow \dfrac{{31}}{{60}}*\dfrac{{22}}{7}*\dfrac{{384400}}{{180}} = AB \\
   \Rightarrow \dfrac{{31}}{6}*\dfrac{{22}}{7}*\dfrac{{3844}}{{18}} = AB \\
   \Rightarrow \dfrac{{31}}{3}*\dfrac{{11}}{7}*\dfrac{{1922}}{9} = AB \\
   \Rightarrow 3464\dfrac{8}{{63}}km = AB \\
$
The diameter of the moon is $3464\dfrac{8}{{63}}km$
The correct option is a.
Note: The distance along the arc (part of the circumference of a circle, or of any curve). For a circle: Arc Length = θ × r. (when θ is in radians) Arc Length = (θ × π/180) × r.
Arc length is the distance between two points along a section of a curve. Determining the length of an irregular arc segment is also called rectification of a curve