Question

Assume \[\pi = \dfrac{{22}}{7}\] unless stated otherwise. Find the capacity in litres of a conical vessel with height 12 cm and slant height 13 cm.

Answer 1

Hint: First, we will find the radius of the cone using Pythagoras theorem. Then, we will use the formula for the capacity/ volume of a conical vessel to find the answer. We will substitute the values in the formula and solve to get the capacity. If we get the capacity in any unit other than litres, we will convert it to litres.
Formula used:
We have use following formulas in this question:
1.\[V = \dfrac{1}{3}\pi {r^2}h\] where \[V\] is the volume, \[h\] is the height and \[r\] is the radius of the conical vessel.
2.In a right angled triangle, \[{P^2} + {B^2} = {H^2}\] where \[P\], \[B\] and \[H\] are the perpendicular, base and hypotenuse of the right angled triangle respectively.

Complete step-by-step answer:
First, we will draw the diagram of a conical vessel.

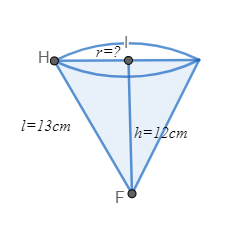
We will apply the Pythagoras theorem in \[\Delta FHI\] which is a right angled triangle. Let us substitute 12 for \[P\], 13 for \[H\]in the formula \[{P^2} + {B^2} = {H^2}\] and let us find \[r\] by simplifying the equation.
\[{P^2} + {B^2} = {H^2}\]
Substituting the values in the above equation, we get
\[ \Rightarrow {12^2} + {r^2} = {13^2}\]
Applying the exponent on the terms, we get
\[\begin{array}{l} \Rightarrow 144 + {r^2} = 169\\ \Rightarrow {r^2} = 169 - 144\end{array}\]
Simplifying the above equation, we get
\[\begin{array}{l} \Rightarrow r = \sqrt {169 - 144} \\ \Rightarrow r = \sqrt {25} \\ \Rightarrow r = 5{\rm{cm}}\end{array}\]

Let us find the capacity of the conical vessel by substituting 12 for \[h\] and 5 for \[r\] in the 1st formula.
\[V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {5^2} \times 12\]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow V = \dfrac{{22 \times 25 \times 12}}{{21}}\\ \Rightarrow V = 314.286{\rm{c}}{{\rm{m}}^3}\end{array}\]
We have got the capacity in \[{\rm{c}}{{\rm{m}}^3}\], let us convert it into litres. We know that \[{\rm{1c}}{{\rm{m}}^3}\] is equivalent to \[0.001l\].
\[314.286{\rm{c}}{{\rm{m}}^3}\] will be equal to \[0.314286l\].

Note: We have to be very careful about the units of the volume that we get. We must not forget to convert it into litres. Alternatively we can also convert the height and radius into decimetre because $1\text{ d}{{\text{m}}^{3}}=1l$ . 1 decimetre is equal to \[0.1\] centimetre.