
Assertion(A): The exponent of prime 5 in 234! is 56.
Reason(R):
If n is a positive integer and p is a prime number, then the exponent of P in n! is given by $\left[ {\dfrac{n}{p}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^2 }}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^3 }}} \right] + ......$
A) Both (A) and (R) are individually true & (R) is a correct explanation of (A).
B) Both (A) and (R) are individually true but (R) is not the correct (proper) explanation of (A).
C) (A) is true but (R) is false.
D) (A) is false but (R) is true.
Answer
594k+ views
Hint: For finding the power of prime p in a factorial; we may write the prime factorization of that number if the number is small or else it would be a tedious task.
For calculating the power of prime in factorial of a larger number $\left( {n!} \right)$; we have to use the result:
Exponent of prime p in $n!$
\[ = \left[ {\dfrac{n}{p}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^2 }}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^3 }}} \right] + ...\],
Where, is the greatest integer function.
Complete step by step answer:
Since the statement given in reason is that if n is a positive integer and p is a prime number, then the exponent of p in n! is given by $\left[ {\dfrac{n}{p}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^2 }}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^3 }}} \right] + ......$, is a standard result.
The reason is a correct statement.
The exponent of prime 5 in 234!
\[ = \left[ {\dfrac{{234}}{5}} \right] + \left[ {\dfrac{{234}}{{\mathop 5\nolimits^2 }}} \right] + \left[ {\dfrac{{234}}{{\mathop 5\nolimits^3 }}} \right] + ...\]
up to the greatest integer gives 0.
$\dfrac{{234}}{5} = 46.8 \Rightarrow \left[ {\dfrac{{234}}{5}} \right] = 46$
\[\dfrac{{234}}{{\mathop 5\nolimits^2 }} = \dfrac{{234}}{{25}} = 9.36 \Rightarrow \left[ {\dfrac{{234}}{{25}}} \right] = 9\]
\[\dfrac{{234}}{{\mathop 5\nolimits^3 }} = \dfrac{{234}}{{125}} = 1.872 \Rightarrow \left[ {\dfrac{{234}}{{125}}} \right] = 1\]
\[\dfrac{{234}}{{\mathop 5\nolimits^4 }} = \dfrac{{234}}{{625}} = 0.37 \Rightarrow \left[ {\dfrac{{234}}{{625}}} \right] = 0\]
Since, \[\left[ {\dfrac{{234}}{{\mathop 5\nolimits^4 }}} \right]\] gives 0, we need not to find further as those will also give result 0.
$\therefore $exponent of 5 in 234! = 46 + 9 + 1
= 56.
Thus, the assertion is also true.
$\therefore$ Both Assertion (A) and Reason (R) are individually true and the reason is a correct explanation of the assertion. Thus, the correct option is (A).
Additional information:
The question uses the greatest integer function, the greatest integer function rounds off the real number to an integer less than the number.
For example: $\left[ {5.12} \right] = 5$
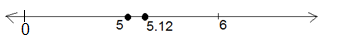
$\left[ {3.96} \right] = 3$

$\left[ { - 1.44} \right] = 2$

Gives the greatest integer less than the given number.
Note:
In the given question, calculation can be made easier if we divide the result of step 1) (that is, $\dfrac{{234}}{5} = 46.8$) by 5 rather than step 2) (that is, \[\dfrac{{234}}{{\mathop 5\nolimits^2 }} = \dfrac{{234}}{{25}}\]) which will save us a lot of time and avoid calculation errors.
Thus, we may proceed as follows:
$\dfrac{{234}}{5} = 46.8 \Rightarrow \left[ {\dfrac{{234}}{5}} \right] = 46$
\[\dfrac{{46}}{5} = 9.2 \Rightarrow \left[ {\dfrac{{46}}{5}} \right] = 9 = \left[ {\dfrac{{234}}{{\mathop 5\nolimits^2 }}} \right]\]
\[\dfrac{9}{5} = 1.8 \Rightarrow \left[ {\dfrac{9}{5}} \right] = 1 = \left[ {\dfrac{{234}}{{\mathop 5\nolimits^3 }}} \right]\]
For calculating the power of prime in factorial of a larger number $\left( {n!} \right)$; we have to use the result:
Exponent of prime p in $n!$
\[ = \left[ {\dfrac{n}{p}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^2 }}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^3 }}} \right] + ...\],
Where, is the greatest integer function.
Complete step by step answer:
Since the statement given in reason is that if n is a positive integer and p is a prime number, then the exponent of p in n! is given by $\left[ {\dfrac{n}{p}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^2 }}} \right] + \left[ {\dfrac{n}{{\mathop p\nolimits^3 }}} \right] + ......$, is a standard result.
The reason is a correct statement.
The exponent of prime 5 in 234!
\[ = \left[ {\dfrac{{234}}{5}} \right] + \left[ {\dfrac{{234}}{{\mathop 5\nolimits^2 }}} \right] + \left[ {\dfrac{{234}}{{\mathop 5\nolimits^3 }}} \right] + ...\]
up to the greatest integer gives 0.
$\dfrac{{234}}{5} = 46.8 \Rightarrow \left[ {\dfrac{{234}}{5}} \right] = 46$
\[\dfrac{{234}}{{\mathop 5\nolimits^2 }} = \dfrac{{234}}{{25}} = 9.36 \Rightarrow \left[ {\dfrac{{234}}{{25}}} \right] = 9\]
\[\dfrac{{234}}{{\mathop 5\nolimits^3 }} = \dfrac{{234}}{{125}} = 1.872 \Rightarrow \left[ {\dfrac{{234}}{{125}}} \right] = 1\]
\[\dfrac{{234}}{{\mathop 5\nolimits^4 }} = \dfrac{{234}}{{625}} = 0.37 \Rightarrow \left[ {\dfrac{{234}}{{625}}} \right] = 0\]
Since, \[\left[ {\dfrac{{234}}{{\mathop 5\nolimits^4 }}} \right]\] gives 0, we need not to find further as those will also give result 0.
$\therefore $exponent of 5 in 234! = 46 + 9 + 1
= 56.
Thus, the assertion is also true.
$\therefore$ Both Assertion (A) and Reason (R) are individually true and the reason is a correct explanation of the assertion. Thus, the correct option is (A).
Additional information:
The question uses the greatest integer function, the greatest integer function rounds off the real number to an integer less than the number.
For example: $\left[ {5.12} \right] = 5$
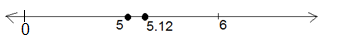
$\left[ {3.96} \right] = 3$

$\left[ { - 1.44} \right] = 2$

Gives the greatest integer less than the given number.
Note:
In the given question, calculation can be made easier if we divide the result of step 1) (that is, $\dfrac{{234}}{5} = 46.8$) by 5 rather than step 2) (that is, \[\dfrac{{234}}{{\mathop 5\nolimits^2 }} = \dfrac{{234}}{{25}}\]) which will save us a lot of time and avoid calculation errors.
Thus, we may proceed as follows:
$\dfrac{{234}}{5} = 46.8 \Rightarrow \left[ {\dfrac{{234}}{5}} \right] = 46$
\[\dfrac{{46}}{5} = 9.2 \Rightarrow \left[ {\dfrac{{46}}{5}} \right] = 9 = \left[ {\dfrac{{234}}{{\mathop 5\nolimits^2 }}} \right]\]
\[\dfrac{9}{5} = 1.8 \Rightarrow \left[ {\dfrac{9}{5}} \right] = 1 = \left[ {\dfrac{{234}}{{\mathop 5\nolimits^3 }}} \right]\]
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





