Question

As the planet revolves from point P to point Q, the velocity of the planet:

A. increases
B. decreases
C. remains same
D. remains equal in magnitude but opposite in direction

Answer 1

Hint:
The above problem can be resolved using the concept and the mathematical formula for the orbital velocity. One can define the orbital velocity as that magnitude of velocity, which is possessed by any heavenly object, especially planets while moving around the sun's orbits. The orbital velocity gives an inverse square root relation for the distance from the planet to the sun's centre, which is analysed accordingly.

Complete step by step solution
The planets have the tendency to revolve around the sun and the magnitude of velocity possessed by the planets are typically called orbital velocity.
The expression for the orbital velocity is given as,
\[{v_o} = \sqrt {\dfrac{{GM}}{r}} \]
Here, G is the universal gravitational constant, M is the mass of sun and r is the distance of the planet to the centre of the sun.
The above relation clears that for the constant value of gravitational constant and the mass of the sun. The orbital velocity varies as,
\[{v_o} \propto \dfrac{1}{{\sqrt r }}\]
The distance is in inverse relation with the velocity.
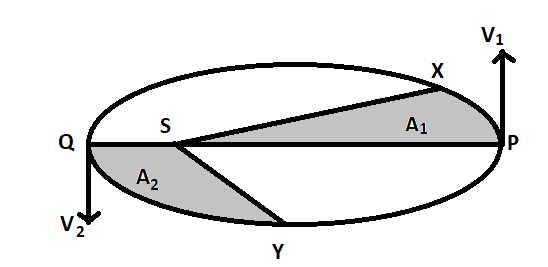
And as the distance SP is greater than the distance SQ, the velocity at Q is more than that at point P.
Therefore, the velocity increases from point P to Q and option (A) is correct.


Note:
To resolve the given problem, one must go through the concepts involving the planet's orbital speed. The orbital speed of any planet depends on the mass of any object around which such a revolution takes place. Along with this, the practical significance of the orbital speed is to be remembered.