Question

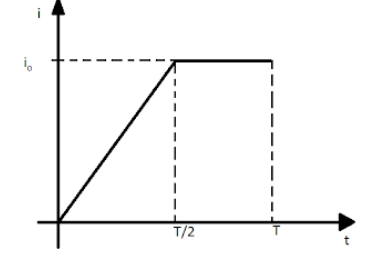
As shown in the graph, the R.M.S value of the current is $ \sqrt {\dfrac{2}{x}} {i_0} $ . Find $ x $ .

A) 1
B) 5
C) 7
D) None of the above

Answer 1

Hint: In order to solve this question, we are first going to take the general formula for the RMS value of the current and fin the value using the value given at the time $ t = \dfrac{T}{2} $ , then, equating it to the given value, we can easily find the value of the variable $ x $ as we need to find.
The root mean square value of the current can be calculated using the formula
 $ {i_{RMS}} = \dfrac{{{i_m}}}{{\sqrt 2 }} $
Where, $ {i_m} $ is the value of the peak current.

Complete answer:
It is given that at time $ t = \dfrac{T}{2} $ , the value of the current is
 $ i = {i_0} $
Now, the formula for the RMS value of current is given by
 $ {i_{RMS}} = \dfrac{{{i_m}}}{{\sqrt 2 }} $
Where, $ {i_m} $ is the value of the peak current.
Putting the values, we get
 $ {i_{RMS}} = \dfrac{{{i_0}}}{{\sqrt 2 }} $
Equating this value to the RMS current as given in the question i.e. $ \sqrt {\dfrac{2}{x}} {i_0} $
This implies
 $ \dfrac{{{i_0}}}{{\sqrt 2 }} = \sqrt {\dfrac{2}{x}} {i_0} \\
   \Rightarrow x = \sqrt 2 \times \sqrt 2 = 2 \\ $
Thus, the value of $ x $ obtained in here does not match any of the options.
Hence, the option (D), “None of the above”, is the correct answer.

Note:
The RMS value is the effective value of a varying voltage or current. It is the equivalent steady DC (constant) value which gives the same effect. Mathematically, it depends only on the peak value of the current and is equal to the $ \dfrac{1}{{\sqrt 2 }} $ times the value of the peak current. The significance of the RMS value is such that a lamp with the RMS voltage $ 6V\, $ will shine with the same brightness as the same value of DC current.