Question

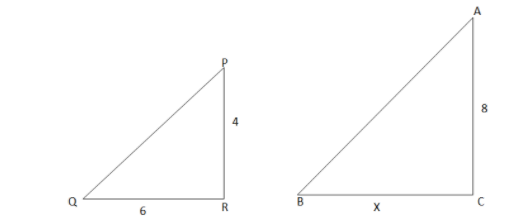
As shown in the figure , two poles of height 8 m and 4 m are perpendicular to the ground. If the length of the shadow of the smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

Answer 1

Hint: Here we have to find the length of the shadow of the long pole. The angle made by sunlight at the top of both poles will be the same and both poles are perpendicular to the ground. From there, we will get two angels of the triangles equal. Therefore, the two triangles will be similar by AA criteria of similarity.
Thus, the ratio of the sides of the triangle will be equal. After evaluation, we will get the length of the shadow of the bigger pole.

Complete step by step solution:
Given:
$
  PR = 4m \\
  AC = 8m \\
  QR = 6m \\
  BC = x \\
 $
We have to find the length of the shadow of the long pole i.e. we have to find the length of$BC$, which is $x$ m here.
The angles made by the sunlight at the top of the two poles are equal i.e. angle of depression of both the poles are equal.
Therefore,
$\angle QPR = \angle BAC..........\left( 1 \right)$
Also, both the poles are perpendicular to the ground.
Therefore,
$\angle PRQ = \angle ACB = {90^ \circ }...........\left( 2 \right)$
In $\vartriangle PQR\& \vartriangle ABC$, we have
$\angle QPR = \angle BAC$ (Angle made by the sunlight at the top of the poles is equal)
$\angle PRQ = \angle ACB = {90^ \circ }$(Poles are perpendicular to the poles)
Thus, these two triangles are similar by AA criteria of similarity.
Therefore, the ratio of the corresponding sides of the triangles will be equal.
The ratio of the side PR to side AC is equal to the ratio of the side QR to side BC as the two triangles are similar.
$\dfrac{{PR}}{{AC}} = \dfrac{{QR}}{{BC}}$
Putting value of side PR, QR, BC and AC, we get
$\Rightarrow$ $\dfrac{4}{8} = \dfrac{6}{x}$
On cross multiplying the terms, we get
$\Rightarrow$ $x = 12m$
Hence, the length of the shadow of the bigger pole is 12 m.

Note: Two triangles are said to be similar if they have the same shape but they can have different sizes.
(i)Some important properties of similar triangles are as follows:-
(ii)The corresponding angles of the similar triangles are of the same measure.
(iii)The corresponding sides of similar triangles are in proportion i.e. the ratio of their corresponding sides are equal.