Question

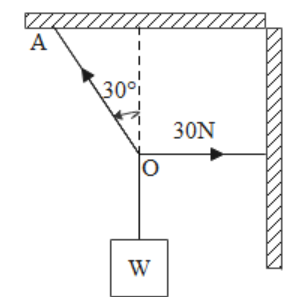
As shown in the figure, the tension in the horizontal cord is 30N. The weight w and tension in the string OA in newton are:

$\begin{align}
  &{\text{A}}{\text{. 30}}\sqrt 3 ,{\text{ 30}} \\
 & {\text{B}}{\text{. 30}}\sqrt 3 ,{\text{ 60}} \\
 & {\text{C}}{\text{. 60}}\sqrt 3 ,{\text{ 30}} \\
  &{\text{D}}{\text{. none of the above}} \\
\end{align} $

Answer 1

Hint: First we need to draw a free body diagram which will show all the forces acting on the system. Then by equating various components, we shall obtain equations will be able to give us the desired values of tension and weight

Complete step-by-step solution:
Let us first draw all the forces acting on the given system by drawing a free body diagram in the following way.

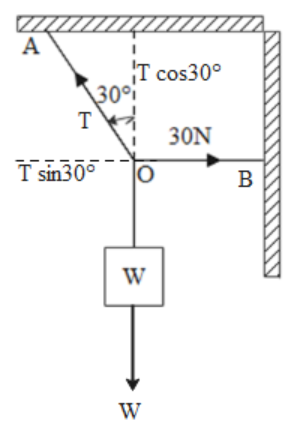
In the diagram, we have resolved the tension T in the string OA into its horizontal and vertical components.
We are given that the tension in the horizontal cord OB is 30N. Based on the various forces which we can see in the diagram, we can say that
1. The weight W of the block is balanced by the vertical component \[T\cos 30^\circ \] of the tension in the string OA. Therefore, we can write the following expression.
$\begin{align}
  &T\cos 30^\circ = W \\
 &\Rightarrow W = \dfrac{{\sqrt 3 }}{2}T \\
\end{align} $ …(i)
2. The tension of 30N in the string OB is balanced by the horizontal component \[T\sin 30^\circ \] of the tension in the string OA. Therefore, we can write the following expression.
$\begin{align}
& T\sin 30^\circ = 30 \\
 &\Rightarrow \dfrac{T}{2} = 30 \\
&\Rightarrow T = 60N \\
\end{align} $
Now we will use this value of tension in equation (i) to find out the value of weight W. This is done in the following way.
$W = \dfrac{{\sqrt 3 }}{2} \times 60 = 30\sqrt 3 N$
These are the required values asked in the question. Hence, the correct answer is option B.

Note: The various forces and components that we are equating in our solution are taken as the magnitude of the forces which are canceling each other. This cancellation ensures that the system stays fixed. The directions of the various forces canceling each other are in opposite directions to each other.