Question

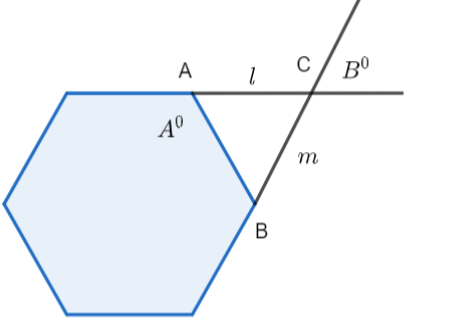
As shown in the below figure, the two sides of the regular hexagon when extended meet at the intersection of the lines l and m. If the measure of angle A is 120 degrees, then the measure of angle B, in degree, is:

\[\begin{align}
  & (A)\text{ }30 \\
 & (B)\text{ }60 \\
 & (C)\text{ }90 \\
 & (D)\text{ }140 \\
\end{align}\]

Answer 1

Let us assume the triangle formed by lines l and m as \[\Delta ABC\] with vertices A, B, and C respectively. We know that the angle on a straight line is 180 degrees. By this statement, we will find the \[\angle BAC\]. As the given hexagon is a regular hexagon, each and every angle is equal to 120 degrees. In a similar way, we will find the \[\angle ABC\]. We know that the sum of angles in a triangle is equal to 180 degrees. By this, we can find \[\angle BCA\]. By this, the concept of angle on a straight line is 180 degrees. We will find the exterior angles of \[\angle BCA\]. In a similar manner, we will find the angle B in degrees.

Complete step-by-step solution:
From the question, it was given that the two sides of the regular hexagon when extended meet at the intersection of the lines l and m.
The lines l and m form a triangle. Let us assume this triangle as \[\Delta ABC\] with vertices A, B, and C respectively.

From the question, it was given that the measure of angle A is 120 degrees. We know that the angle on a straight line is 180 degrees. So, the sum of \[\angle BAC\]and \[{{A}^{{}^\circ }}\] is equal to \[{{180}^{{}^\circ }}\].
\[\begin{align}
  & \Rightarrow \angle BAC+{{A}^{{}^\circ }}={{180}^{{}^\circ }} \\
 & \Rightarrow \angle BAC+{{120}^{{}^\circ }}={{180}^{{}^\circ }} \\
 & \Rightarrow \angle BAC={{60}^{{}^\circ }}....(1) \\
\end{align}\]
In the question, it was given that all angles in a regular hexagon are equal to 120 degrees. So, the exterior angle of \[\angle ABC\] is equal to 120 degrees.
So, on line m we get
\[\begin{align}
  & \Rightarrow \angle ABC+{{120}^{{}^\circ }}={{180}^{{}^\circ }} \\
 & \Rightarrow \angle ABC={{60}^{{}^\circ }}....(2) \\
\end{align}\]
We know that the sum of all angles in a triangle is equal to 180 degrees.
So, we get
From equation (1) and equation (2) we get
\[\begin{align}
  & \Rightarrow {{60}^{{}^\circ }}+{{60}^{{}^\circ }}+\angle BCA={{180}^{{}^\circ }} \\
 & \Rightarrow \angle BCA={{180}^{{}^\circ }}-{{120}^{{}^\circ }} \\
 & \Rightarrow \angle BCA={{60}^{{}^\circ }}....(3) \\
\end{align}\]
We know that the angle on a straight line is 180 degrees. So, the sum of \[\angle BCA\] and exterior angle of \[\angle BCA\] in triangle ABC is equal to \[{{180}^{{}^\circ }}\].
Let us assume the exterior angle of \[\angle BCA\] as \[{{C}^{{}^\circ }}\].
From equation (3), we get
\[\begin{align}
  & \Rightarrow \angle BCA+{{C}^{{}^\circ }}={{180}^{{}^\circ }} \\
 & \Rightarrow {{C}^{{}^\circ }}={{180}^{{}^\circ }}-\angle BCA \\
 & \Rightarrow {{C}^{{}^\circ }}={{180}^{{}^\circ }}-{{60}^{{}^\circ }} \\
 & \Rightarrow {{C}^{{}^\circ }}={{120}^{{}^\circ }}....(4) \\
\end{align}\]
In a similar manner, the sum of \[{{C}^{{}^\circ }}\] and \[{{B}^{{}^\circ }}\] is equal to 180.
From equation (4), we get
\[\begin{align}
  & \Rightarrow {{C}^{{}^\circ }}+{{B}^{{}^\circ }}={{180}^{{}^\circ }} \\
 & \Rightarrow {{B}^{{}^\circ }}={{180}^{{}^\circ }}-{{120}^{{}^\circ }} \\
 & \Rightarrow {{B}^{{}^\circ }}={{60}^{{}^\circ }}....(5) \\
\end{align}\]
So, from equation (5) it is clear that measure of angle B is equal to 60 degrees.
Hence, option (B) is correct.

Note: There can be chances of mistakes while solving the question. So, apply each property properly and avoid making any calculation errors. They must understand that since a regular hexagon is given, all the interior angles of the regular hexagon will be 120 degrees. After obtaining the angle $\angle BCA={{60}^{\circ }}$, we can also use the fact that angles $\angle BCA={{60}^{\circ }}$ and \[{{B}^{{}^\circ }}\] are vertically opposite to each other, so they would be equal. Hence, the last part can be solved in this manner too.